Washington Taking Command of the Army
Although he did not explicitly seek the office of commander and even claimed that he was not equal to…

Seal of Wyoming
The Great Seal of the State of Wyoming. The seal shows two men symbolizing livestock and mining next…

Section of the King's Chamber
At the end of the lengthy series of entrance ways leading into the interior is the structure's main…
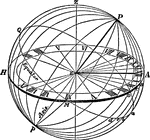
Horizontal Dial
The chief advantages of the horizontal sundial are that it is easy to read, and the sun lights the face…

Sundial
A sundial is a device that measures time by the position of the Sun. In common designs such as the horizontal…
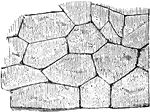
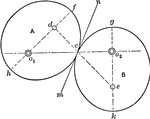
Cyclopean Masonry
Remains of the circular walls round towns and palaces, which are known under the name Cyclopean, exist…

The Lion Gate at Mycenæ
Remains of the circular walls round towns and palaces, which are known under the name Cyclopean, exist…

Doric Order Frieze in the Parthenon at Athens
The frieze of the Doric order is not taken up with sculpture in uninterrupted succession, but it occurs…

Roman Square Panel
The Roman square panels is an 1879 bas-relief design found near the Tiber river in Rome, Italy. This…

Assyrian Pavement Square Panel
The Assyrian pavement square panel is a divided into eight equal spaces that are decorated with a repeated…

Greek Square Panel
The Greek square panel is found on the coffer of the Propylaea ceiling, the entrance to the Acropolis…

Greek Square Panel
The Greek square panel is found on the coffer of the Propylaea ceiling, the entrance to the Acropolis…

Greek Square Panel
The Greek square panel is found in Athens. This panel is divided into eight equal spaces that are decorated…

Greek Square Panel
The Greek square panel is found on the coffer of the Parhtenon ceiling, a Greek Temple. This panel is…

Decorated Square Panel
This decorated square panel is found on a 10th century book. This panel is divided into eight equal…

Scandinavian Square Panel
The Scandinavian square panel is a bas-relief design found on a Celtic stone cross. This panel is divided…
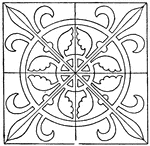
Medieval Square Panel
The Medieval square panel is a tile that is divided into eight equal spaces that are decorated with…
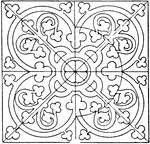
Medieval Square Panel
The Medieval square panel is a tile that is divided into eight equal spaces that are decorated with…

Medieval Square Panel
The Medieval square panel is a tile that is divided into eight equal spaces that are decorated with…
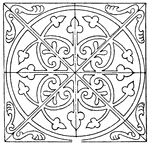
Medieval Square Panel
The Medieval square panel is a tile that is divided into eight equal spaces that are decorated with…
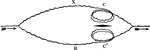
Differential Galvanometer
"The galvanometer consists of two distinct coils of wire, each having the same resistance, and having…
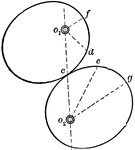
Rolling of Non-cylindrical Surfaces
Illustration showing that the rolling of non-cylindrical surfaces. "If the angular velocity ratio of…
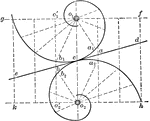
Rolling of Logarithmic Spirals
Illustration showing the rolling of two logarithmic spirals of equal obliquity.
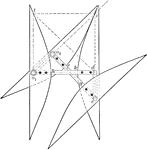
Rolling of Equal Ellipses
"If two equal ellipses, each turning about one of its foci, are placed in contact in such a way that…

Rolling of Equal Parabolas
Illustration of the rolling of equal parabolas. "The two parabolas may be considered as two ellipses…
Rolling of Equal Hyperbolas
Illustration of the rolling of equal hyperbolas. If two equal hyperbolas are placed so that the distances…
Ambiguous Case
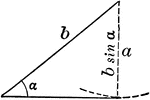
Illustration of one possible outcome (1 triangle occurs) when discussing the ambiguous case using the…
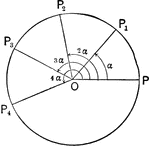
Geometric Inspection of Complex Numbers
Illustration showing complex numbers with a modulus equal to unity. The lines representing these numbers…

Funnel-shaped Brass
A funnel-shaped piece of brass is placed over the ends of a galvanometer when the resistance is equal…
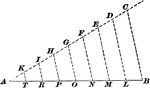
Construction Of Dividing A Line
Illustration used to show how to divide a given straight line into required number of equal parts.
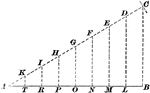
Construction Of Dividing A Line
Illustration used to show how to divide a given straight line into required number of equal parts.
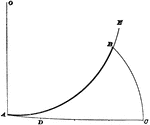
Construction Of Arc
Illustration used to show how to "find an arc of a circle having a known radius, which shall be equal…

Construction Of Line Equal To Arc
Illustration used to show how to find a straight line of the same length as a given arc of a circle.
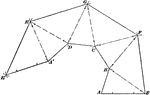
Irregular Solid With Triangular Surfaces
Illustration of an irregular solid form made up of triangular surfaces unfolded on a flat surface. A…
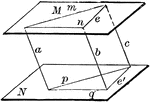
Angles In Parallel Planes
"If two angles not in the same plane have their sides respectively parallel and lying in the same direction,…
Oyster Shell
An illustration of a oyster shell. The common name oyster is used for a number of different groups of…
Oyster Shell
An illustration of a oyster shell. The common name oyster is used for a number of different groups of…

Oyster Shell
An illustration of a oyster shell. The common name oyster is used for a number of different groups of…

Cube with Additions 1
A cube (A) has sides of 20 inches in length each, making its solid contents equal 8000 cubic inches.…

Obverse and Reverse Sides of Farthing of Charles II
The obverse and reverse sides of the farthing depicting Charles II. The farthing was an English coin…
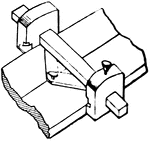
Bisecting Gauge
"Bisecting gage, a gage formed by a bar carrying two heads or cheeks connected by two arms of equal…
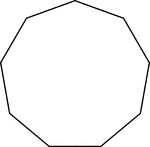
Regular Nonagon
Illustration of a regular nonagon. A nonagon is a closed geometric figure with 9 sides. A regular nonagon…

Symmetrical or Equal Trihedral Angles
Diagram used to prove the theorem: "Two trihedral angles, which have three face angles of the one equal…

Lateral Area of A Prism
Diagram used to prove the theorem: "The lateral area of a prism is equal to the product of a lateral…
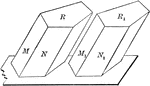
Two Equal Prisms
Diagram used to prove the theorem: "Two prisms are equal when the three faces about a trihedral of one…
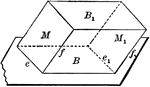
Equal and Parallel Opposite Faces of a Parallelopiped
Diagram used to prove the theorem: "The opposite faces of a parallelopiped are equal and parallel."
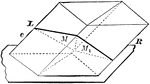
Parallelopiped Divided Into Triangular Prisms
Diagram used to prove the theorem: "The plane passed through two diagonally opposite edges of a parallelopiped…
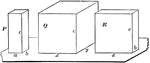
Relationship Between 2 Parallelopipeds With Equal Altitudes
Diagram used to prove the theorem: "The rectangular parallelopipeds which have two dimensions in common…

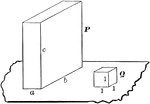
Relationship Between Dimensions of Parallelopipeds
Diagram used to prove the theorem: "The rectangular parallelopipeds are to each other as the product…
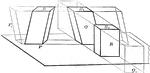
Volume of Rectangular Parallelopiped
Diagram used to prove the theorem: "The volume of a rectangular parallelopiped is equal to the product…
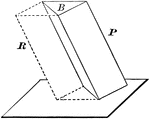
Volume of Parallelopiped
Diagram used to prove the theorem: "The volume of a any parallelopiped is equal to the product of its…
Volume of Triangular Prism
Diagram used to prove the theorem: "The volume of a triangular prism is equal to the product of its…
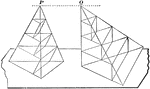
Equivalent Triangular Pyramids
Diagram used to prove the theorem: "Two triangular pyramids having equivalent bases and equal altitudes…

Volume of Triangular Pyramid
Diagram used to prove the theorem: "The volume of a triangular pyramid is equal to one third of a triangular…
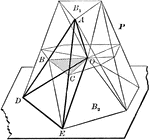
Volume of Prismatoid
Diagram used to prove the theorem: "The volume of a prismatoid is equal to the product of one-sixth…