Flashcard of a Pyramid with a Triangular Base
A flashcard featuring an illustration of a Pyramid with a Triangular Base

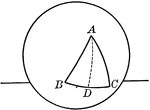
Right Triangle
Illustration of a right triangle used to show the Pythagorean Theorem (the square of the hypotenuse…
Hexagon Used to Construct Equivalent Triangle
Illustration of a how to construct a triangle equivalent to a given hexagon/polygon.

Plane Passing Through the Vertex of a Cone
Illustration of a plane passing through the vertex of a cone (section made is a triangle).

Plane Passing Through the Vertex of a Cone
Illustration of a plane passing through the vertex of a cone (section made is a triangle).

Equal Spheres With Triangles
Illustration of equal spheres with equilateral and equiangular triangles.

Tangents and Chords of a Parabola
Illustration showing that the area of a parabolic segment made by a chord is two thirds the area of…

Right Triangle Showing Pythagorean Theorem
Illustration of a right triangle that can be used to show Pythagorean theorem. "In any right triangle,…
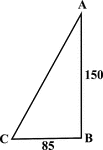
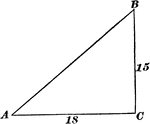
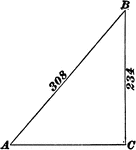
Right Triangle With Sides 85 and 150
Illustration of a right triangle with legs labeled 150 and 85. This could be used to find the hypotenuse…

Similar Triangles
Illustration of a triangle divided by a parallel line to form two similar triangles.
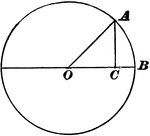
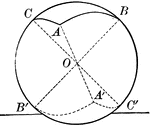
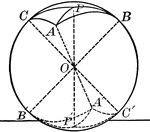
Trigonometry Triangle to Show Sine, Cosine, and Tangent
Right triangle OCA, inside of Circle O is used to show that side AC is "opposite" O and side OC is "adjacent"…
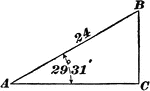
Triangle With Angle of 29 ° 31' and Side of 24
Right triangle with angle of 29 ° 31' and side of 24.
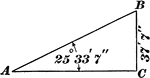
Triangle With Angle of 25 ° 33' 7" and Side of 37' 7"
Right triangle with angle of 25 ° 33' 7" and side of 37' 7"
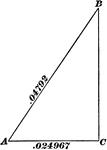
Right Triangle With Side .024967 and Hypotenuse .04792
Right triangle with side .024967 and hypotenuse .04792.
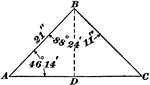
Oblique Triangle With Side 21' and Angles 88 ° 24' 11" and 46 ° 14'
Oblique triangle with side 21' and angles 88 ° 24' 11" and 46 ° 14'.
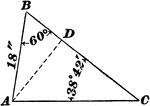
Oblique Triangle With Side 18" and Angles 60 ° and 38 ° 42'
Oblique triangle with side 18" and angles 60 ° and 38 ° 42'.
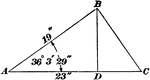
Oblique Triangle With Perpendicular Drawn
Oblique triangle with perpendicular drawn to form two right triangles, one with angle measuring 36 °…
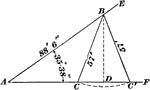
Oblique Triangle Used For Ambiguous Case
Oblique triangle with perpendicular drawn and angle of measure 35 ° 38" given, and sides of 88'…
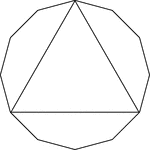
Triangle Inscribed In A Dodecagon
Illustration of an equilateral triangle inscribed in an equilateral dodecagon. This could also be described…

12 Triangles Inscribed In A Dodecagon
Illustration of 12 equilateral triangles inscribed in an equilateral dodecagon. Each vertex of the dodecagon…
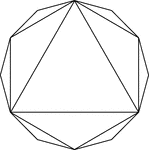
Hexagon And Triangle Inscribed In A Dodecagon
Illustration of a regular hexagon and an equilateral triangle inscribed in a regular dodecagon. This…

3 Yin Yang Design Symbols In A Circle
Design made by drawing one large circle and then three circles that are internally tangent to the original…

3 Yin Yang Design Symbols In A Circle
Design made by drawing one large circle and then three circles that are internally tangent to the original…

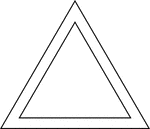
Equilateral Triangle Inscribed In An Equilateral Triangle
Illustration of an equilateral triangle inscribed in an equilateral triangle. The smaller triangle is…
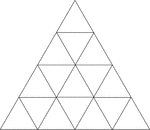
Equilateral Triangles Inscribed In An Equilateral Triangle
Illustration of an equilateral triangle inscribed in an equilateral triangle by joining the midpoints…
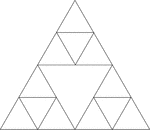
Equilateral Triangles Inscribed In Equilateral Triangles
Illustration of an equilateral triangle inscribed in an equilateral triangle by joining the midpoints…
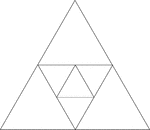
Equilateral Triangles Inscribed In Equilateral Triangles
Illustration of an equilateral triangle inscribed in an equilateral triangle by joining the midpoints…
3 Concentric Equilateral Triangles
Illustration of 3 concentric equilateral triangles that are equally spaced.

4 Concentric Equilateral Triangles
Illustration of 4 concentric equilateral triangles that are equally spaced.
Centers of Equilateral Triangle
Illustration of an equilateral triangle that shows both the centroid (where the medians of the sides…
10 Congruent Rotated Equilateral Triangles
Illustration of 10 congruent equilateral triangles that have the same center. Each triangle has been…
10 Congruent Rotated Equilateral Triangles
Illustration of 10 congruent equilateral triangles that have the same center. Each triangle has been…

5 Congruent Rotated Equilateral Triangles
Illustration of 5 congruent equilateral triangles that have the same center. Each triangle has been…
20 Congruent Rotated Equilateral Triangles
Illustration of 20 congruent equilateral triangles that have the same center. Each triangle has been…

3 Ladders Leaning Against a Wall
Illustration of 3 ladders leaning against the side of a building (wall) to form right triangles. The…
Extension Ladder
Illustration of an extension ladder. If ladder is leaned against a building, it will form a right triangle…
Leaning Ladder
Illustration of a ladder that is not perpendicular to the ground. If it is set on the ground and leaned…