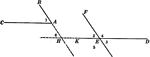
2 Angles With Parallel Sides Theorem
Illustration used to prove the theorem, "Two angles whose sides are parallel, each to each, are either…
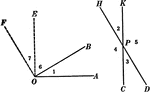
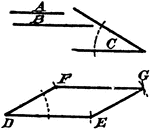
2 Angles With Perpendicular Sides Theorem
Illustration used to prove the theorem, "Two angles whose sides are perpendicular, each to each, are…
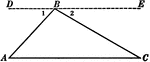
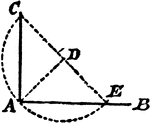
Sum Of Angles In Triangle Theorem
Illustration used to prove the theorem, "The sum of the angles of any triangle is two right angles."
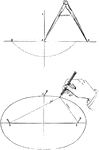
Construction Of An Ellipse
Illustrations used to construct an ellipse. Fig. 59 shows a compass at C used to strike a circle. Where…
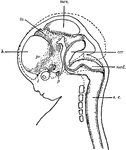
Human Fetus
"Diagram of head and brain of human foetus six weeks old (heavy boundaries). The dotted line indicates…
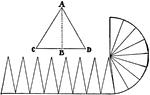
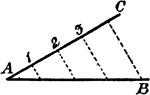
Area of Circle with Triangles
"In the triangle above, the line AB is its altitude. Since we know how to find the area of one triangle,…
Construction Of A Line Divided In Equal Parts
An illustration showing the construction used to divide a line AB into two equal parts; and to erect…
Construction Of A Perpendicular
An illustration showing the construction used to erect a perpendicular from a point to a line. "With…
Construction Of A Perpendicular
An illustration showing the construction used to erect a perpendicular at the end of a line. "With the…
Construction Of A Parallel
An illustration showing the construction used to erect a parallel line. "With C as a center, draw the…
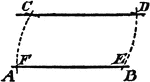
Construction Of A Parallelogram
An illustration showing the construction used to erect a parallelogram given two sides and an angle.…
Divide A Line Proportionately
An illustration showing the construction used to divide the line AB in the same proportion of parts…
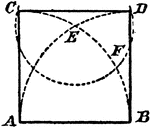
Square Constructed Upon A Given Line
An illustration showing how to construct a square upon a given line. "With AB as radius and A and B…
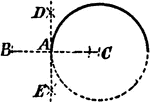
Construction Of Tangent To Circle
An illustration showing how to construct a tangent to a circle through a given point in a circumference.…
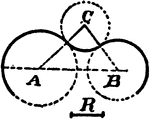
Construction Of Circle Tangent To 2 Circles
An illustration showing how to construct a tangent circle to 2 given circles. "Join centers C and c…

Ptolemy in Profile
He was a mathematician, geographer, astronomer, and astrologer. "The name of a line Graeco-Egyptain…
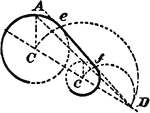
Construction Of Tangent To 2 Circles
An illustration showing how to construct a tangent to 2 given circles of different diameters. "Join…
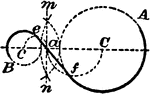
Construction Of Tangent Between 2 Circles
An illustration showing how to construct a tangent between 2 given circles. "Join the centers C and…
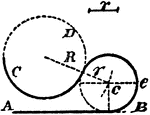
Construction Of A Circle Tangent To A Line And A Circle
An illustration showing how to construct a circle tangent to a given line and given circle. "Add the…
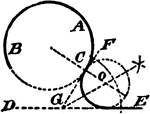
Construction Of A Center And Radius Of A Circle That Will Tangent A Given Circle
An illustration showing how to construct the center and radius of a circle that will tangent a given…
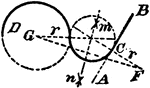
Construction Of A Center And Radius Of A Circle That Will Tangent A Given Circle And Line
An illustration showing how to construct the center and radius of a circle that will tangent a given…
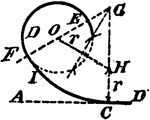
Construction Of A Center And Radius Of A Circle That Will Tangent A Given Circle And Line
An illustration showing how to construct the center and radius of a circle that will tangent a given…
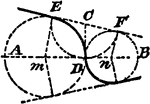
Construction Of Two Circles That Tangent Themselves and 2 Given Lines
An illustration showing how to construct two circles that tangent themselves and two given lines. "Draw…
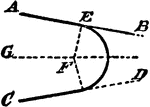
Construction Of A Circle That Tangents 2 Given Lines
An illustration showing how to construct a circle that tangents two given lines inclined to one another…
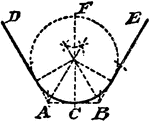
Construction Of A Circle That Tangents 2 Given Lines And Goes Through A Given Point
An illustration showing how to construct a circle that tangents two given lines and goes through a given…
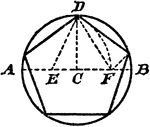
Construction Of A Pentagon Inscribed In A Circle
An illustration showing how to construct a pentagon inscribed in a circle. "Draw the diameter AB, and…
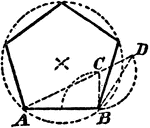
Construction Of A Pentagon On A Line
An illustration showing how to construct a pentagon on a given line. "From B erect BC perpendicular…
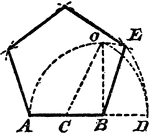
Construction Of A Pentagon On A Line
An illustration showing how to construct a pentagon on a given line without resort to its center. "From…
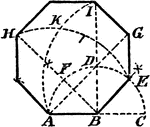
Construction Of An Octagon
An illustration showing how to construct an octagon on a given line. "Prolong AB to C. With B as center…
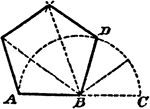
Construction Of A Regular Polygon On A Line
An illustration showing how to construct a regular polygon on a given line without resort to its center.…
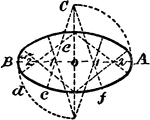
Construction Of An Isometric Ellipse
An illustration showing how to construct an isometric ellipse by compass and six circle arcs. "Divide…

Construction Of Shield's Anti-friction Curve
An illustration showing how to construct Shield's anti-friction curve. "R represents the radius of the…
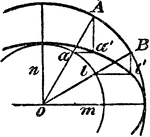
Construction Of An Ellipse
An illustration showing how to construct an ellipse. "With a as a center, draw two concentric circles…
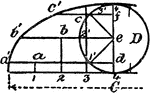
Construction Of A Cycloid
An illustration showing how to construct a cycloid. "The circumference C=3.14D. Divide the rolling circle…
Quadrilateral Inscribed In A Circle
An illustration showing a quadrilateral inscribed in a circle that is tangent to a line.
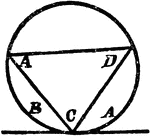
Triangle Inscribed In A Circle
An illustration showing a triangle with angles A, C, and D inscribed in a circle which is tangent to…

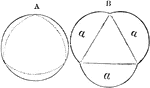
Comparisons Chart
This chart of comparisons can be used with the following questions: "Which line is twice B? Which two…
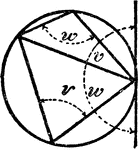
Model Of Geometric Relationships In A Circle
An illustration showing a model of a circle with an exterior angle formed between a tangent and a secant…
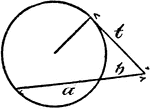
Model Of Geometric Relationships In A Circle
An illustration showing a model of a circle with angles formed between tangents and secants that illustrates…
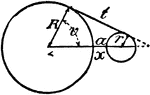
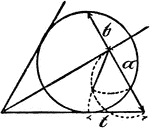
Model Of Geometric Relationships In 2 Circles
An illustration showing a model of 2 circles with tangent lines, diameters, and radii that illustrates…
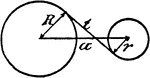
Model Of Geometric Relationships In 2 Circles
An illustration showing a model of 2 circles with tangent lines, diameters, and radii that illustrates…
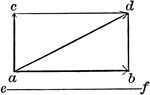
Vector Motion Into Two Components - Resultant
Illustration used to resolve a motion into two components, one of which is perpendicular, and the other…

Velocities Of Rigidly-connected Points
Illustration for rigidly-connected points. "If two points are so connected that their distance apart…
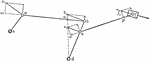
Velocities Of Rigidly-connected Points
Illustration for rigidly-connected points. In the series of links shown, c and d are fixed axes and…
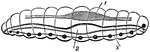
Diagram of an Annulosa
A diagram of an annulosa showing its external skeleton made up of segments or rings arranged along a…

The Superficial Muscles of a Hawk
In birds the muscles system is remarkable for their marked line of attachment to their tendons. Labels:…

A Side View of the Chest and Abdomen in Respiration
A side view of the chest and abdomen in respiration. Labels: 1, The cavity of the chest. 2, The cavity…
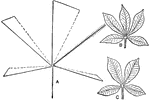
Leaflet Removal
"Effect of removal of a leaflet from a palmately compound leaf (e.g. Woodbine). B, normal leaf; C, after…
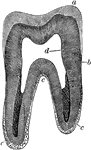
Vertical Section of a Molar
Vertical section of a molar tooth. Labels: a, enamel of the crown, the line of which indicate the arrangement…

Muscle Fiber
Diagram of the appearance in fresh muscle fiber. Labels: A, At low focus (B) the muscle columns appear…
Action of Semilunar Valve
Section of the aorta, to show the action of the semilunar valve. A is intended to show the valves, represented…

Movement of Ribs
The axes of rotation of rib movement is two; one corresponding with a line drawn through two articulations…
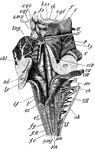
Medulla
Dorsal or posterior view of the medulla, fourth ventricle, and mesencephalon. Labels: p.n., line of…
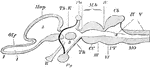
Vertical Section of a Vertebrate Brain
Longitudinal and vertical diagrammatic section of a vertebrate brain. Mb, midbrain: what lies in front…
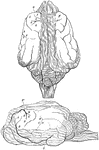
Brain of a Dog
Brain of dog, viewed from above and in profile. F, frontal fissure sometimes termed crucial sulcus,…
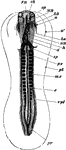
Embryo Chick
Embryo chick (36 hours), viewed from beneath as a transparent object (magnified). Labels:pl, outline…
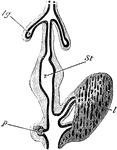
Digestive Tract of a Chick
Diagram of part of digestive tract of a chick (4th day). The black line represents hypoblast , the outer…
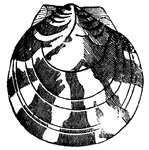
Pecten Pseudamussium (Chenu.)
"The Watered Pecten belongs to the scallop-shells. The shell is generally nearly circular, more or less…

