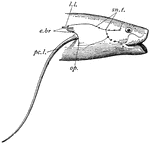
African Lungfish Head
"Head region of Protopterus. sn.t., Sensory tubes; l.l., lateral line; e.br., external gills; pc.l.,…
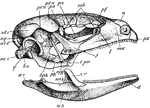
Lizard Skull
"Side view of skull of Lacerta. px., Premaxilla; mx., maxilla; l., lachrymal; j., jugal; t.pa., transpalatine;…
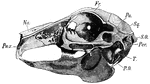
Rabbit Skull
"Side view of rabbit's skull. Pmx., Premaxilla; Na., nasal; Fr., frontal; Pa., parietal; Sq., squamosal;…
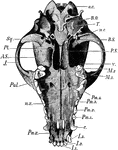
Dog Skull
"Lower surface of dog's skull. o.c., Occipital condyle; B.O., basioccipital; T., tympanic bulla; m.c.,…
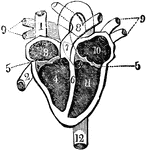
Heart and its Chambers
View of the heart with its several chambers exposed and the vessels in connection with them. Labels:…

Cnidaria
"Sections of types Coelenterates (diagrammatic): 1 (longitudinal) and 2 (transverse) of a tubular hydroid;…
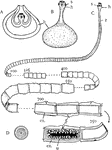
Tapeworm
"Diagram showing some stages in the life history of the Tapeworm (taenia). A, Cysticercus or Bladderworm…

Construction Of A Perpendicular Bisector Of A Straight Line
Illustration of the construction used to make a perpendicular bisector of a straight line.
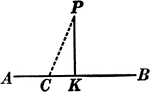
Construction Of A Perpendicular To A Straight Line
Illustration of the construction used to create a perpendicular to a straight line at a given point.
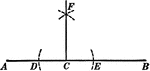
Construction Of A Perpendicular To A Straight Line
Illustration of the construction used to create a perpendicular to a straight line from a given point…
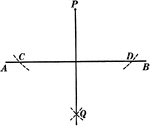
Perpendicular to Line Corollary
Illustration used to prove the corollary that "From a point outside a line there exists only one perpendicular…
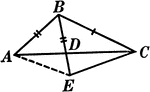
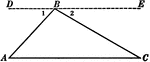
Segments and Angles in a Triangle
Illustration of a triangle with interior segments and angles labeled.
Segments and Angles in a Triangle
Illustration of a triangle with interior segments and angles labeled.
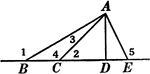
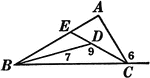
Segments Labeled In A Triangle
Illustration of triangle ABC with BE extended through the triangle at point D. Segment AB is equal to…
Parallel Lines Theorem
Illustration used to prove that "If two straight lines are parallel to a third straight line, they are…
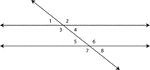
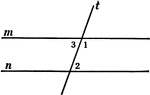
2 Lines Cut By A Transversal
Illustration of two straight lines cut by a transversal. The 8 angles formed are labeled.
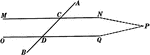
Parallel Lines Cut By A Transversal Theorem
Illustration used to prove the theorem, "If two straight lines are cut by a transversal making a pair…
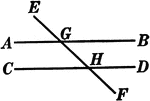
2 Lines Cut By A Transversal
Illustration of two straight lines, AB and CD, cut by a transversal EF.
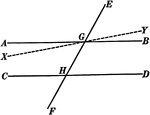
Construction Of A Parallel Line
Illustration of the construction used to create a line parallel to a given line.
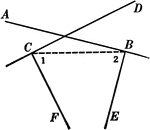
Parallel Lines Cut By A Transversal Theorem
Illustration used to prove the theorem, "If two parallel lines are cut by a transversal, the alternate…
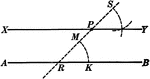
Intersecting Lines Corollary
Illustration used to prove the corollary that "Two lines perpendicular respectively to two intersecting…
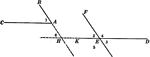
2 Angles With Parallel Sides Theorem
Illustration used to prove the theorem, "Two angles whose sides are parallel, each to each, are either…
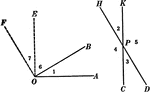
2 Angles With Perpendicular Sides Theorem
Illustration used to prove the theorem, "Two angles whose sides are perpendicular, each to each, are…
Sum Of Angles In Triangle Theorem
Illustration used to prove the theorem, "The sum of the angles of any triangle is two right angles."
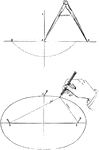
Construction Of An Ellipse
Illustrations used to construct an ellipse. Fig. 59 shows a compass at C used to strike a circle. Where…
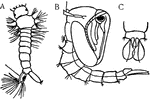
Mosquito Metamorphosis
"Two stages in the metamorphosis of the Mosquito. A, larva; B, pupa; C, ventral view of the oar-like…
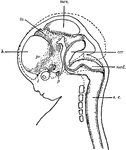
Human Fetus
"Diagram of head and brain of human foetus six weeks old (heavy boundaries). The dotted line indicates…
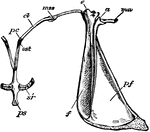
Rabbit Shoulder Girdle
"Lepus cuniculus. Shoulder-girdle with anterior end of sternum of young specimen. a, acromion; af, pre-scapular…
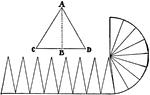
Area of Circle with Triangles
"In the triangle above, the line AB is its altitude. Since we know how to find the area of one triangle,…
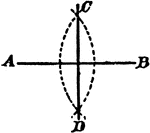
Construction Of A Line Divided In Equal Parts
An illustration showing the construction used to divide a line AB into two equal parts; and to erect…
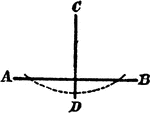
Construction Of A Perpendicular
An illustration showing the construction used to erect a perpendicular from a point to a line. "With…
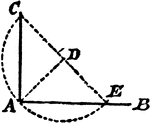
Construction Of A Perpendicular
An illustration showing the construction used to erect a perpendicular at the end of a line. "With the…
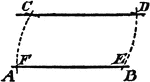
Construction Of A Parallel
An illustration showing the construction used to erect a parallel line. "With C as a center, draw the…
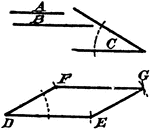
Construction Of A Parallelogram
An illustration showing the construction used to erect a parallelogram given two sides and an angle.…
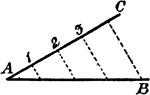
Divide A Line Proportionately
An illustration showing the construction used to divide the line AB in the same proportion of parts…
Square Constructed Upon A Given Line
An illustration showing how to construct a square upon a given line. "With AB as radius and A and B…
Construction Of Tangent To Circle
An illustration showing how to construct a tangent to a circle through a given point in a circumference.…
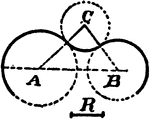
Construction Of Circle Tangent To 2 Circles
An illustration showing how to construct a tangent circle to 2 given circles. "Join centers C and c…

Ptolemy in Profile
He was a mathematician, geographer, astronomer, and astrologer. "The name of a line Graeco-Egyptain…
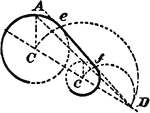
Construction Of Tangent To 2 Circles
An illustration showing how to construct a tangent to 2 given circles of different diameters. "Join…
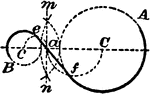
Construction Of Tangent Between 2 Circles
An illustration showing how to construct a tangent between 2 given circles. "Join the centers C and…
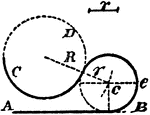
Construction Of A Circle Tangent To A Line And A Circle
An illustration showing how to construct a circle tangent to a given line and given circle. "Add the…
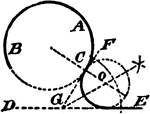
Construction Of A Center And Radius Of A Circle That Will Tangent A Given Circle
An illustration showing how to construct the center and radius of a circle that will tangent a given…
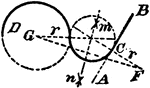
Construction Of A Center And Radius Of A Circle That Will Tangent A Given Circle And Line
An illustration showing how to construct the center and radius of a circle that will tangent a given…
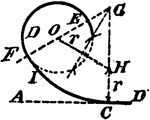
Construction Of A Center And Radius Of A Circle That Will Tangent A Given Circle And Line
An illustration showing how to construct the center and radius of a circle that will tangent a given…
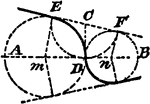
Construction Of Two Circles That Tangent Themselves and 2 Given Lines
An illustration showing how to construct two circles that tangent themselves and two given lines. "Draw…
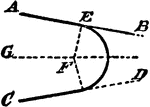
Construction Of A Circle That Tangents 2 Given Lines
An illustration showing how to construct a circle that tangents two given lines inclined to one another…
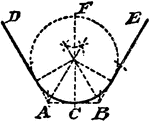
Construction Of A Circle That Tangents 2 Given Lines And Goes Through A Given Point
An illustration showing how to construct a circle that tangents two given lines and goes through a given…
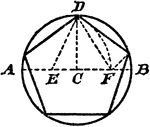
Construction Of A Pentagon Inscribed In A Circle
An illustration showing how to construct a pentagon inscribed in a circle. "Draw the diameter AB, and…
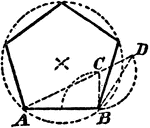
Construction Of A Pentagon On A Line
An illustration showing how to construct a pentagon on a given line. "From B erect BC perpendicular…
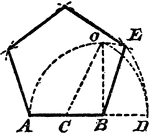
Construction Of A Pentagon On A Line
An illustration showing how to construct a pentagon on a given line without resort to its center. "From…
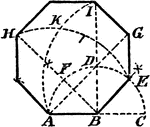
Construction Of An Octagon
An illustration showing how to construct an octagon on a given line. "Prolong AB to C. With B as center…
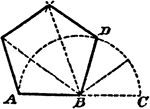
Construction Of A Regular Polygon On A Line
An illustration showing how to construct a regular polygon on a given line without resort to its center.…
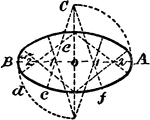
Construction Of An Isometric Ellipse
An illustration showing how to construct an isometric ellipse by compass and six circle arcs. "Divide…

Construction Of Shield's Anti-friction Curve
An illustration showing how to construct Shield's anti-friction curve. "R represents the radius of the…
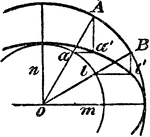
Construction Of An Ellipse
An illustration showing how to construct an ellipse. "With a as a center, draw two concentric circles…
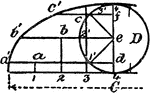
Construction Of A Cycloid
An illustration showing how to construct a cycloid. "The circumference C=3.14D. Divide the rolling circle…
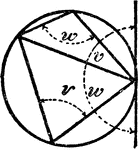
Quadrilateral Inscribed In A Circle
An illustration showing a quadrilateral inscribed in a circle that is tangent to a line.