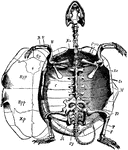
Marsh Turtle Skeleton
"Cistudo lutaria. Skeleton seen from below; the plastron has been removed and is represented on one…
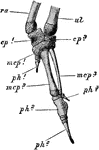
Rock Pigeon Manus
"Columba livia. Left manus of a nestling. The cartilaginous parts are dotted. cp. 1, radiale; cp. 2,…

Circle Parts
A circle with labels for radius, diameter, and circumference. The visual will help to remember what…

Pie Graph
A pie graph of "Proportion of World's Supply of Cotton contributed by each country" labeled with country…
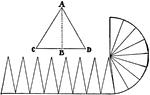
Area of Circle with Triangles
"In the triangle above, the line AB is its altitude. Since we know how to find the area of one triangle,…

Arc of Circle
An illustration of an arc of a circle. An arc is any part of the circumference of a circle.
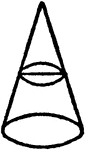
Conic Section Showing A Circle
An illustration showing the intersection of a plane and a cone. The cone is intersected by a plane parallel…
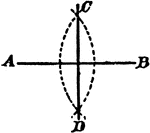
Construction Of A Line Divided In Equal Parts
An illustration showing the construction used to divide a line AB into two equal parts; and to erect…
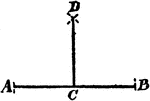
Construction Of A Perpendicular
An illustration showing the construction used to erect a perpendicular. "With C as a center, draw the…
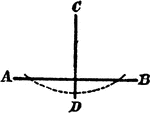
Construction Of A Perpendicular
An illustration showing the construction used to erect a perpendicular from a point to a line. "With…
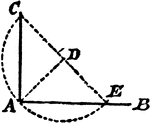
Construction Of A Perpendicular
An illustration showing the construction used to erect a perpendicular at the end of a line. "With the…
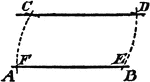
Construction Of A Parallel
An illustration showing the construction used to erect a parallel line. "With C as a center, draw the…
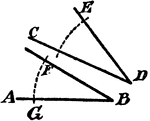
Construction Of An Equal Angle
An illustration showing the construction used to erect an equal angle. "With D as a center, draw the…
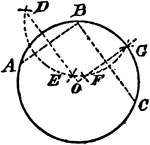
Find The Center Of A Circle Through 3 Points
An illustration showing how to find the center of a circle which will pass through three given points…
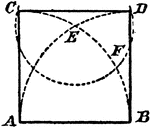
Square Constructed Upon A Given Line
An illustration showing how to construct a square upon a given line. "With AB as radius and A and B…
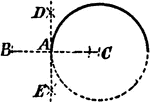
Construction Of Tangent To Circle
An illustration showing how to construct a tangent to a circle through a given point in a circumference.…
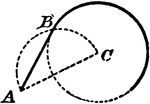
Construction Of Tangent To Circle
An illustration showing how to construct a tangent to a circle through a given point outside of a circumference.…
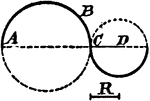
Construction Of Circle Tangent To Circle
An illustration showing how to construct a tangent circle to a circle with a given radius. "Through…
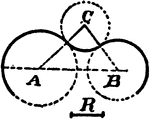
Construction Of Circle Tangent To 2 Circles
An illustration showing how to construct a tangent circle to 2 given circles. "Join centers C and c…
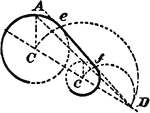
Construction Of Tangent To 2 Circles
An illustration showing how to construct a tangent to 2 given circles of different diameters. "Join…
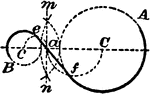
Construction Of Tangent Between 2 Circles
An illustration showing how to construct a tangent between 2 given circles. "Join the centers C and…
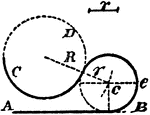
Construction Of A Circle Tangent To A Line And A Circle
An illustration showing how to construct a circle tangent to a given line and given circle. "Add the…
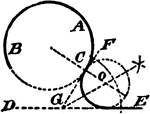
Construction Of A Center And Radius Of A Circle That Will Tangent A Given Circle
An illustration showing how to construct the center and radius of a circle that will tangent a given…
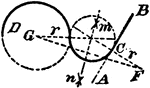
Construction Of A Center And Radius Of A Circle That Will Tangent A Given Circle And Line
An illustration showing how to construct the center and radius of a circle that will tangent a given…
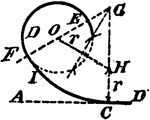
Construction Of A Center And Radius Of A Circle That Will Tangent A Given Circle And Line
An illustration showing how to construct the center and radius of a circle that will tangent a given…
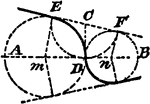
Construction Of Two Circles That Tangent Themselves and 2 Given Lines
An illustration showing how to construct two circles that tangent themselves and two given lines. "Draw…
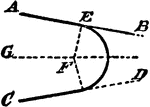
Construction Of A Circle That Tangents 2 Given Lines
An illustration showing how to construct a circle that tangents two given lines inclined to one another…
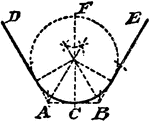
Construction Of A Circle That Tangents 2 Given Lines And Goes Through A Given Point
An illustration showing how to construct a circle that tangents two given lines and goes through a given…
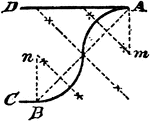
Construction Of A Cyma
An illustration showing how to construct a cyma, or two circle arcs that will tangent themselves, and…
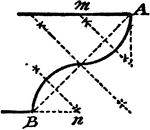
Construction Of A Talon
An illustration showing how to construct a talon, or two circle arcs that will tangent themselves, and…
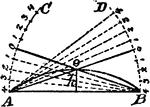
Construction Of A Circle Arc
An illustration showing how to construct a circle arc without recourse to its center, but its chord…
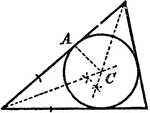
Construction Of The Center And Radius Of A Circle Tangent To Triangle Sides
An illustration showing how to construct a center and radius of a circle that will tangent the three…

Construction Of An Equilateral Triangle Inscribed In A Circle
An illustration showing how to construct an equilateral triangle inscribed in a circle. "With the radius…
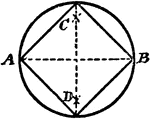
Construction Of A Square Inscribed In A Circle
An illustration showing how to construct a square inscribed in a circle. "Draw the diameter AB, and…

Construction Of A Square Circumscribed About A Circle
An illustration showing how to construct a square circumscribed about a circle. "Draw the diameters…
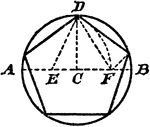
Construction Of A Pentagon Inscribed In A Circle
An illustration showing how to construct a pentagon inscribed in a circle. "Draw the diameter AB, and…
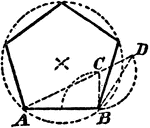
Construction Of A Pentagon On A Line
An illustration showing how to construct a pentagon on a given line. "From B erect BC perpendicular…
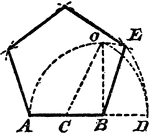
Construction Of A Pentagon On A Line
An illustration showing how to construct a pentagon on a given line without resort to its center. "From…
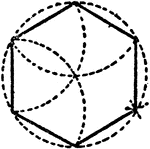
Construction Of A Hexagon In A Circle
An illustration showing how to construct a hexagon in a given circle. "The radius of the circle is equal…
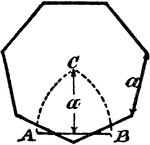
Construction Of A Heptagon
An illustration showing how to construct a heptagon, or septagon. "The appotem a in a hexagon is the…
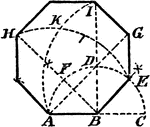
Construction Of An Octagon
An illustration showing how to construct an octagon on a given line. "Prolong AB to C. With B as center…
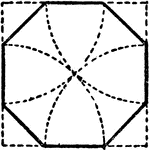
Construction Of An Octagon From a Square
An illustration showing how to construct a regular octagon from a square by cutting off the corners…
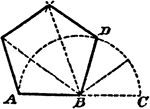
Construction Of A Regular Polygon On A Line
An illustration showing how to construct a regular polygon on a given line without resort to its center.…
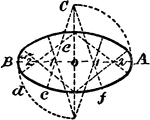
Construction Of An Isometric Ellipse
An illustration showing how to construct an isometric ellipse by compass and six circle arcs. "Divide…
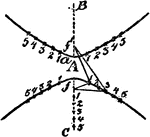
Construction Of A Hyperbola
An illustration showing how to construct a hyperbola by plotting. "Having given the transverse axis…

Construction Of Shield's Anti-friction Curve
An illustration showing how to construct Shield's anti-friction curve. "R represents the radius of the…
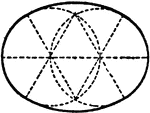
Construction Of An Ellipse
An illustration showing how to construct an ellipse using circle arcs. "Divide the long axis into three…
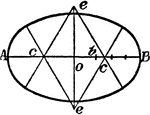
Construction Of An Ellipse
An illustration showing how to construct an ellipse using circle arcs. "Given the two axes, set off…
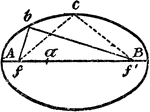
Construction Of An Ellipse
An illustration showing how to construct an ellipse. Given the two axes, set off half the long axis…
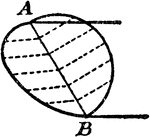
Construction Of An Ellipse Tangent To Two Parallel Lines
An illustration showing how to construct an ellipse parallel to two parallel lines A and B. "Draw a…
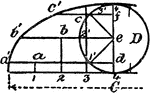
Construction Of A Cycloid
An illustration showing how to construct a cycloid. "The circumference C=3.14D. Divide the rolling circle…

Construction Of An Evolute Of A Circle
An illustration showing how to construct an evolute of a circle. "Given the pitch p, the angle v, and…
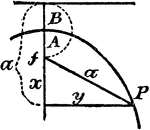
Construction Of A Parabola
An illustration showing how to construct a parabola. "Given the axis of ordinate B, and vertex A. Take…

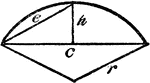
Radius, Diameter, and Chord In A Circle
An illustration showing a circle with radius r, diameter d, and chord c.
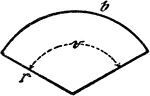
Circle Sector
An illustration showing a circle sector with radius r, center/central angle v, and length of circle…

Circle Sector
An illustration showing a circle sector with center/central angle v and polygon angle w.
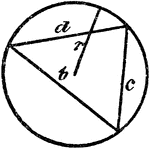
Triangle Inscribed In A Circle
An illustration showing a triangle with sides b, c, and d inscribed in a circle with radius r.
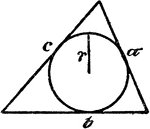
Circle Inscribed In A Triangle
An illustration showing a circle with radius r inscribed in a triangle with sides a, b, and c.