180° and -180° Coterminal Angles
Illustration showing coterminal angles of 180° and -180°. Coterminal angles are angles drawn…
185° and -175° Coterminal Angles
Illustration showing coterminal angles of 185° and -175°. Coterminal angles are angles drawn…
190° and -170° Coterminal Angles
Illustration showing coterminal angles of 190° and -170°. Coterminal angles are angles drawn…
195° and -165° Coterminal Angles
Illustration showing coterminal angles of 195° and -165°. Coterminal angles are angles drawn…
200° and -160° Coterminal Angles
Illustration showing coterminal angles of 200° and -160°. Coterminal angles are angles drawn…
205° and -155° Coterminal Angles
Illustration showing coterminal angles of 205° and -155°. Coterminal angles are angles drawn…
210° and -150° Coterminal Angles
Illustration showing coterminal angles of 210° and -150°. Coterminal angles are angles drawn…
215° and -145° Coterminal Angles
Illustration showing coterminal angles of 215° and -145°. Coterminal angles are angles drawn…
220° and -140° Coterminal Angles
Illustration showing coterminal angles of 220° and -140°. Coterminal angles are angles drawn…
225° and -135° Coterminal Angles
Illustration showing coterminal angles of 225° and -135°. Coterminal angles are angles drawn…
230° and -130° Coterminal Angles
Illustration showing coterminal angles of 230° and -130°. Coterminal angles are angles drawn…
235° and -125° Coterminal Angles
Illustration showing coterminal angles of 235° and -125°. Coterminal angles are angles drawn…
240° and -120° Coterminal Angles
Illustration showing coterminal angles of 240° and -120°. Coterminal angles are angles drawn…
245° and -115° Coterminal Angles
Illustration showing coterminal angles of 245° and -115°. Coterminal angles are angles drawn…
250° and -110° Coterminal Angles
Illustration showing coterminal angles of 250° and -110°. Coterminal angles are angles drawn…
255° and -105° Coterminal Angles
Illustration showing coterminal angles of 255° and -105°. Coterminal angles are angles drawn…
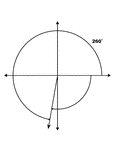
260° and -100° Coterminal Angles
Illustration showing coterminal angles of 260° and -100°. Coterminal angles are angles drawn…
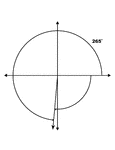
265° and -95° Coterminal Angles
Illustration showing coterminal angles of 265° and -95°. Coterminal angles are angles drawn…
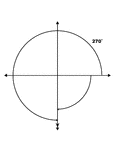
270° and -90° Coterminal Angles
Illustration showing coterminal angles of 270° and -90°. Coterminal angles are angles drawn…
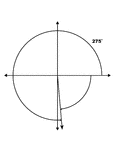
275° and -85° Coterminal Angles
Illustration showing coterminal angles of 275° and -85°. Coterminal angles are angles drawn…

280° and -80° Coterminal Angles
Illustration showing coterminal angles of 280° and -80°. Coterminal angles are angles drawn…
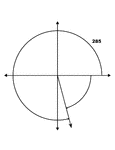
285° and -75° Coterminal Angles
Illustration showing coterminal angles of 285° and -75°. Coterminal angles are angles drawn…
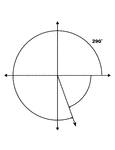
290° and -70° Coterminal Angles
Illustration showing coterminal angles of 290° and -70°. Coterminal angles are angles drawn…
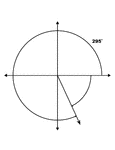
295° and -65° Coterminal Angles
Illustration showing coterminal angles of 295° and -65°. Coterminal angles are angles drawn…
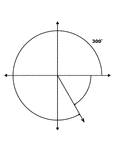
300° and -60° Coterminal Angles
Illustration showing coterminal angles of 300° and -60°. Coterminal angles are angles drawn…
305° and -55° Coterminal Angles
Illustration showing coterminal angles of 305° and -55°. Coterminal angles are angles drawn…
310° and -50° Coterminal Angles
Illustration showing coterminal angles of 310° and -50°. Coterminal angles are angles drawn…

315° and -45° Coterminal Angles
Illustration showing coterminal angles of 315° and -45°. Coterminal angles are angles drawn…
320° and -40° Coterminal Angles
Illustration showing coterminal angles of 320° and -40°. Coterminal angles are angles drawn…
325° and -35° Coterminal Angles
Illustration showing coterminal angles of 325° and -35°. Coterminal angles are angles drawn…
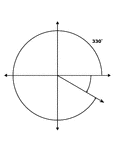
330° and -30° Coterminal Angles
Illustration showing coterminal angles of 330° and -30°. Coterminal angles are angles drawn…
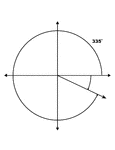
335° and -25° Coterminal Angles
Illustration showing coterminal angles of 335° and -25°. Coterminal angles are angles drawn…
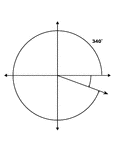
340° and -20° Coterminal Angles
Illustration showing coterminal angles of 340° and -20°. Coterminal angles are angles drawn…
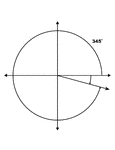
345° and -15° Coterminal Angles
Illustration showing coterminal angles of 345° and -15°. Coterminal angles are angles drawn…

350° and -10° Coterminal Angles
Illustration showing coterminal angles of 350° and -10°. Coterminal angles are angles drawn…
355° and -5° Coterminal Angles
Illustration showing coterminal angles of 355° and -5°. Coterminal angles are angles drawn in…
360° and 0° Coterminal Angles
Illustration showing coterminal angles of 360° and 0°. Coterminal angles are angles drawn in…
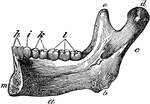
Lower Jaw
Half of the lower jaw. Labels: a, the base; b, the angle; c, the ramus; d, the condyle; e, the coronaid…
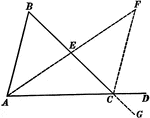
Exterior Angle of Triangle Theorem
Illustration used to prove that "If one side of a triangle is prolonged, the exterior angle formed is…
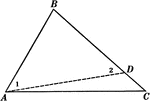
Sides of Triangle Theorem
Illustration used to prove that "If two sides of a triangle are unequal, the angle opposite the greater…
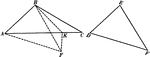
2 Triangles Theorem
Illustration used to prove that "If two triangles have two sides of one equal respectively to two sides…
2 Triangles Theorem
Illustration used to prove that "If two triangles have two sides of one equal respectively to two sides…
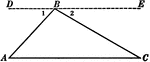
Sum Of Angles In Triangle Theorem
Illustration used to prove the theorem, "The sum of the angles of any triangle is two right angles."

Axillary
"Axillary.--Placed in the axilla (arm-pit). A term by which the angle formed by the union of the leaf…

Castle Parts
"Details of a castle: 1. Fortified approach 2. Drawbridge 3. Moat 4. Donjon or keep 5. Towers flanking…

Gathering, Sugar Cane
"The plant tillers like wheat, but not to the same degree. The cane ground is kept clean by hand-hoeing,…
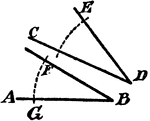
Construction Of An Equal Angle
An illustration showing the construction used to erect an equal angle. "With D as a center, draw the…

Construction Of A Divided Angle
An illustration showing the construction used to divide an angle into two equal parts. "With C as a…
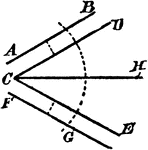
Construction Of A Divided Angle
An illustration showing the construction used to divide an angle into two equal parts when the lines…
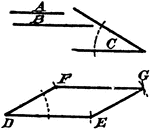
Construction Of A Parallelogram
An illustration showing the construction used to erect a parallelogram given two sides and an angle.…
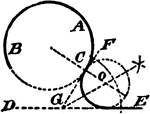
Construction Of A Center And Radius Of A Circle That Will Tangent A Given Circle
An illustration showing how to construct the center and radius of a circle that will tangent a given…
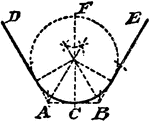
Construction Of A Circle That Tangents 2 Given Lines And Goes Through A Given Point
An illustration showing how to construct a circle that tangents two given lines and goes through a given…
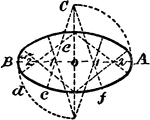
Construction Of An Isometric Ellipse
An illustration showing how to construct an isometric ellipse by compass and six circle arcs. "Divide…

Ravelin
A detached triangular work in fortification, with two embankments which form a projecting angle. In…

Redans
In field fortification, the simplest kind of work employed, consisting of two parapets of earth raised…
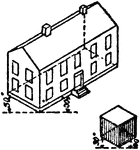
Construction Using Isometric Perspective
An illustration showing how to use isometric perspective. "This kind of perspective admits of scale…
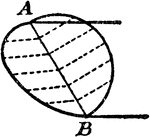
Construction Of An Ellipse Tangent To Two Parallel Lines
An illustration showing how to construct an ellipse parallel to two parallel lines A and B. "Draw a…

Construction Of An Evolute Of A Circle
An illustration showing how to construct an evolute of a circle. "Given the pitch p, the angle v, and…

Construction Of A Parabola
An illustration showing how to construct a parabola. "Given the vertex A, axis x, and a point P. Draw…
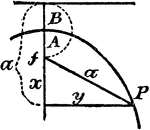
Construction Of A Parabola
An illustration showing how to construct a parabola. "Given the axis of ordinate B, and vertex A. Take…