
Allerion
"Argent, an allerion gules. ALLERION. An eagle displayed, without beak or feet." -Hall, 1862

Argent
"ARGENT. The French word for silver, of which metal all white fields or charges are supposed to consist."…
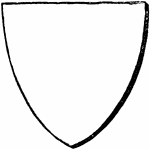
Argent Shield
A heraldic shield made of argent (silver), which is represented by its plain, smooth surface.
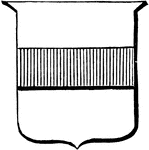
Argent, a Fess Gules
"Argent, a fess gules" describes the red (gules) stripe (fess) on the silver (argent) field.
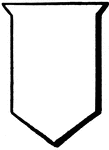
Argent Shield Metal
A shield or escutcheon emblazoned with the metal tincture, argent (silver), represented by white.

Augmentation
"Ermine, on a chevron azure, three foxes' heads erased, argent. The augmentation is in a canton azure,…
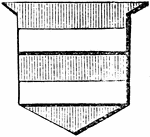
Shield Showing Bar
Argent, two closets, azure. The closet is a diminutive of the bar, and is half its width. -Hall, 1862
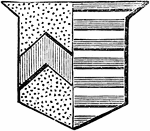
Baron and Femme
"Parted per pale, baron and femme, two coats; first, or, a chevron gules; second, barry of twelve pieces,…

Baron and Femme
"Baron and femme, two atchievements. First, azure, a pile or, crest a star of six points, argent; second,…
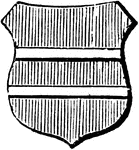
Barrulet Ordinary
"Gules, two barrulets argent. BARRULET. The smallest diminutive of the bar. The closet is half the bar;…

Shield Showing Barrulet
Azure, two bars, gemels, argent. The annexed example is to illustrate the word gemels, which is frequently…

Barry of Seven Pieces
34 And Jephthah came to Mizpeh unto his house, and, behold, his daughter came out to meet him with timbrels…
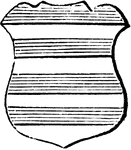
Barry Ordinary
"Barry of eight pieces, azure and argent. BARRY. A field divided transversely into several equal parts,…

Bars Wavy
"Argent, the lower half of the shield three bars wavy, azure. WAVY. Curved lines, undulating like the…
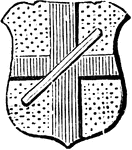
Baton Abatement
"Or, a cross gules, over all a baton argent. BATON. BATUNE. BASTON. It is generally used as an abatement…

Battering Ram
"Argent, a battering ram proper. BATTERING RAM. An instrument used for battering down walls before gunpowder…

Battle Axe
"Argent, three battle axes gules two over one. BATTLE AXE. An ancient military weapon, frequently borne…

Battlement
The white represents silver or "argent," the fesse is the band going across. It is gules or red and…
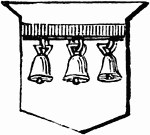
Barrulet Belled
"Argent, a barrulet gules, belled with three bells proper. BELLED. Having bells." -Hall, 1862
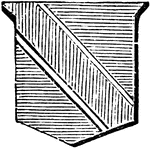
Bend Fimbriated
"Azure, a bend gules, fimbriated argent. FIMBRIATED. An ordinary having a border of a different tincture…
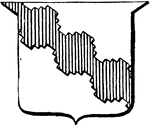
Bend Grady
"Argent, a Bend Grady Gules. GRADY. In heraldry, cut into steps, one upon another: said of lines, of…
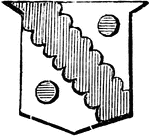
Bend Invected
"Argent, a bend gules, invected between two hurts. INVECTED. A line formed with small semicircles, with…
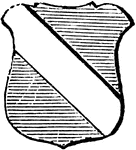
Bend Ordinary
"Azure, a bend argent. BEND. One of the honourable ordinaries formed by two diagonal lines drawn from…
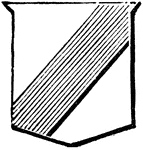
Bend Sinister
Argent, a scarpe, purpure. The scarpe is the diminutive of the bend sinister, and is half its size.…

Bend Sinister
"Argent, a bend sinister gules. BEND SINISTER. Is the reverse of the bend; it is seldom found in coats…

Bend Sinister Embattled
"Gules, a bend sinister embattled, argent. EMBATTLED. A line, formed like the battlements on a wall…
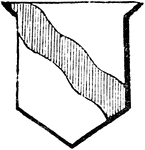
Bend Undy
"Argent, a bend undy, gules. UNDY. A term used to express the word wavy by Gwillim and other ancient…

Ordinary Bend
"Argent, a bend, vert. The bend is an honourable ordinary, formed by two diagonal lines drawn from the…
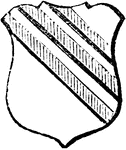
Bendlets Enhanced
"Argent, three bendlets, enhanced gules. ENHANCED. A term applied to bearings placed above their usual…
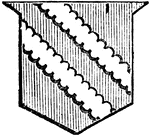
Shield Showing Bendlets
Argent, a bend sinister, purpure. The bend sinister is the same breadth as the bend dexter, and is drawn…

Bendy Ordinary
"Bendy of six pieces, azure and argent. BENDY. This word serves to denote a field divided diagonally…

Billets
"Argent, three billets azure, two over one. BILLETS. This charge is, by some authors, supposed to represent…

Boar Couped
"Argent, a boar's head proper couped. COUPED. The head or limbs of any animal cut close is called couped."…

Boar Tusked
"Argent, a boar's head, erased proper, tusked gules. TUSKED. Any animal having tusks of a different…
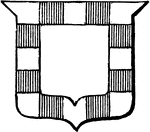
Bordure Gobonated
"A Bordure Gobonated Argent and Gules. GOBONATED. In heraldry, same as componé." -Whitney, 1911

Boujet
"Argent, a boujet proper. BOUJET. An ancient water bucket, frequently borne in shields of arms." -Hall,…
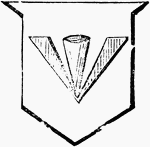
Broad Arrow
"Argent, a broad arrow gules. BROAD ARROW. An ancient weapon of war, thrown by an engine. It is frequently…

Caltrop
"Argent, a caltrop proper. CALTROP. An iron instrument made to annoy an enemy's cavalry. They were formed…
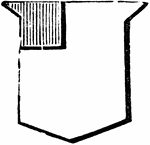
Canton
"CANTON. The French word for corner. It is a small square figure, generally placed at the dexter chief…

Chaplet
"Argent, a chaplet proper. CHAPLET. An ancient ornament for the head, granted to gallant knights for…

Checky
"Checky, sable and argent. CHECKY. The field covered with alternate squares of metal and fur." -Hall,…
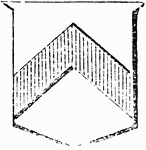
Shield Showing Chevron
Argent, two chevronels, gules. The diminutives of the chevron, according to English Heraldry, are the…

Chevronels
"Argent, two chevronels gules. CHEVRONEL. The diminutive of the chevron, being one half its size." -Hall,…

Shield Showing Chevronels
Gules, three couple-closes interlaced in base, or ... the couple-close ... is half the chevronel. -Hall,…

Chief Indented
"Argent, a chief, azure, indented. The chief is an ordinary terminated by an horizontal line, which,…

Chief Ordinary
"Argent, on a chief, gules, two mullets, sable. The chief is an ordinary terminated by an horizontal…

Shield Showing Closet
Gules, two barrulets, argent. The barrulet is half the width of the closet. -Hall, 1862

Compony
"Argent, an inescutcheon azure, border compony, or and gules. COMPONY. A term applied to a bordure,…
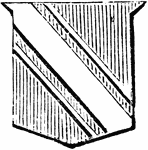
Cotice
"Gules, a bend argent, coticed of the same. COTICE. One of the diminutives of the bend: cotices are…
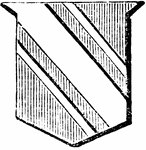
Shield Showing Cotice
Argent, a riband vert. The riband, which is one third less than the garter and the bendlet, must never…
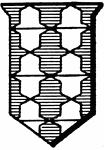
Counter-Vair Shield Fur
A shield or escutcheon emblazoned with the fur, vair, represented by alternating azure (blue) and argent…

Couple-Close
"Argent, three couple-closes interlaced vert. COUPLE-CLOSE. One of the diminutives of the chevron, half…
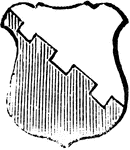
Crescent
"Azure, a crescent argent. CRESCENT. The half moon with its horns turned upwards." -Hall, 1862

Cross
"CROSS. An honourable ordinary, more used as a charge in a coat of arms than any of the others." -Hall,…

Cross Bottonny
"Cross bottonny. CROSS. An honourable ordinary, more used as a charge in a coat of arms than any of…

Cross Couped
"Azure, a cross couped argent. COUPED. From the French word couper, to cut. The cross in the example…

Cross Crosslet
"Cross crosslet. CROSS. An honourable ordinary, more used as a charge in a coat of arms than any of…

Cross Flory
"Cross flory. CROSS. An honourable ordinary, more used as a charge in a coat of arms than any of the…

