Clipart tagged: ‘Circumference’

Golden Angle
Illustration showing the golden angle. The golden angle is the smaller of two angles created by dividing…

Brazilian Trees
This image of a giant Brazilian Tree shows about fifteen men with arms outstretched are needed to embrace…
Construction Of A Center And Radius Of A Circle That Will Tangent A Given Circle And Line
An illustration showing how to construct the center and radius of a circle that will tangent a given…
Construction Of A Center And Radius Of A Circle That Will Tangent A Given Circle And Line
An illustration showing how to construct the center and radius of a circle that will tangent a given…
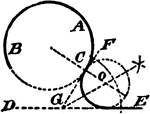
Construction Of A Center And Radius Of A Circle That Will Tangent A Given Circle
An illustration showing how to construct the center and radius of a circle that will tangent a given…
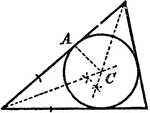
Construction Of The Center And Radius Of A Circle Tangent To Triangle Sides
An illustration showing how to construct a center and radius of a circle that will tangent the three…
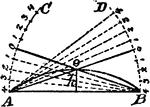
Construction Of A Circle Arc
An illustration showing how to construct a circle arc without recourse to its center, but its chord…

Circle Parts
A circle with labels for radius, diameter, and circumference. The visual will help to remember what…
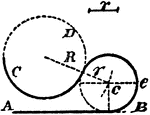
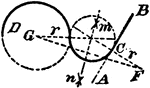
Construction Of A Circle Tangent To A Line And A Circle
An illustration showing how to construct a circle tangent to a given line and given circle. "Add the…
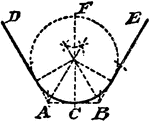
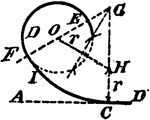
Construction Of A Circle That Tangents 2 Given Lines And Goes Through A Given Point
An illustration showing how to construct a circle that tangents two given lines and goes through a given…
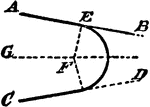
Construction Of A Circle That Tangents 2 Given Lines
An illustration showing how to construct a circle that tangents two given lines inclined to one another…

Arc of Circle
An illustration of an arc of a circle. An arc is any part of the circumference of a circle.
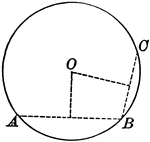
Circle With Circumference Through Three Points
Illustration of a circle which illustrates that through three points not in a straight line one circumference,…

Triangles Making Up A Circle
Illustration showing that a circle may be considered as made up of triangles whose bases form the circumference.
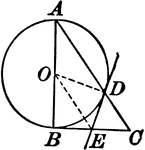
Circle With a Right Triangle
Illustration where one leg of a right triangle is the diameter of a circle. The tangent at the point…
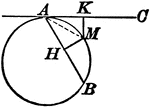
Circle With a Tangent Line and Chord
Illustration showing that from any point in the circumference of a circle, a chord and a tangent are…
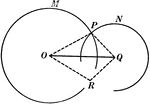
Circumferences of 2 Circles
Illustration used to prove "If two circumferences meet at a point which is not on their line of centers,…
Circles With Parallels Intercepting Equal Arcs
Illustration of a circle with parallels intercepting equal arcs on a circumference.
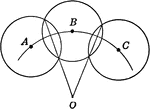
Construction of Radius When Given Only a Part of the Circumference
Illustration of of construction of a radius when given only a part of the circumference.
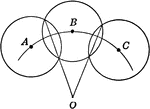
Construction of Radius When Given Only a Part of the Circumference
Illustration of of construction of a radius when given only a part of the circumference.
Cycloid
"A cycloid is the curve generated by the motion of a point on the circumference of a circle rolled along…
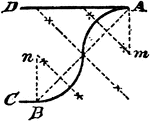
Construction Of A Cyma
An illustration showing how to construct a cyma, or two circle arcs that will tangent themselves, and…

Epicycloid
"In geometry, a curve generated by the motion of a point on the circumference of a circle which rolls…

Epicycloid and Hypocycloid
Epicycloid is generated by a circle rolled outside of another circle, whereas a hypocycloid is circle…
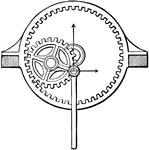
Epicycloidal Wheel
"Epicycloidal wheel, a wheel or ring fixed to a framework, toothed on its inner side, and having in…

Construction Of An Equilateral Triangle Inscribed In A Circle
An illustration showing how to construct an equilateral triangle inscribed in a circle. "With the radius…
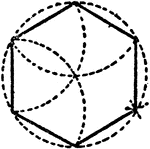
Construction Of A Hexagon In A Circle
An illustration showing how to construct a hexagon in a given circle. "The radius of the circle is equal…
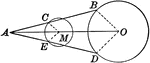
Midpoint of Straight Line Drawn From an Exterior point to Circumference
Illustration showing a line with a midpoint drawn from a given exterior point to a given circumference.

Straight Line Moving to Two circles
Illustration showing a line that remains parallel to a given line, and touches at one end a given circumference.
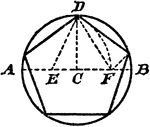
Construction Of A Pentagon Inscribed In A Circle
An illustration showing how to construct a pentagon inscribed in a circle. "Draw the diameter AB, and…
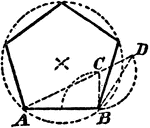
Construction Of A Pentagon On A Line
An illustration showing how to construct a pentagon on a given line. "From B erect BC perpendicular…

Circumference of a Circle of a Sphere
Diagram used to prove the theorem: "All points in the circumference of a circle of a sphere are equally…

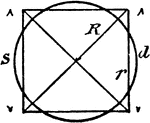
Construction Of A Square Circumscribed About A Circle
An illustration showing how to construct a square circumscribed about a circle. "Draw the diameters…
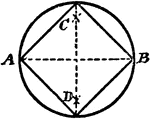
Construction Of A Square Inscribed In A Circle
An illustration showing how to construct a square inscribed in a circle. "Draw the diameter AB, and…
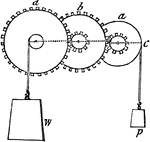
System of Wheels
"System of Wheels.—As the wheel and axle is only a modification of the simple lever, so a system…
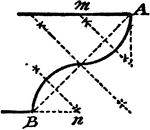
Construction Of A Talon
An illustration showing how to construct a talon, or two circle arcs that will tangent themselves, and…
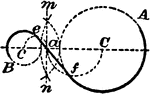
Construction Of Tangent Between 2 Circles
An illustration showing how to construct a tangent between 2 given circles. "Join the centers C and…
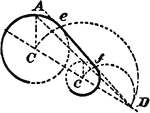
Construction Of Tangent To 2 Circles
An illustration showing how to construct a tangent to 2 given circles of different diameters. "Join…
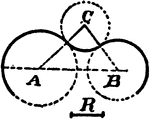
Construction Of Circle Tangent To 2 Circles
An illustration showing how to construct a tangent circle to 2 given circles. "Join centers C and c…
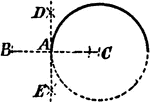
Construction Of Tangent To Circle
An illustration showing how to construct a tangent to a circle through a given point in a circumference.…
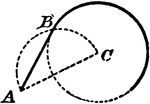
Construction Of Tangent To Circle
An illustration showing how to construct a tangent to a circle through a given point outside of a circumference.…
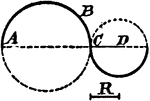
Construction Of Circle Tangent To Circle
An illustration showing how to construct a tangent circle to a circle with a given radius. "Through…
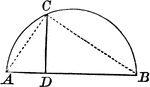
Right Triangle Inscribed in Semicircle Shows Mean Proportional
Right triangle inscribed in semicircle. Illustration shows that the perpendicular from any point in…
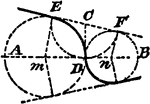
Construction Of Two Circles That Tangent Themselves and 2 Given Lines
An illustration showing how to construct two circles that tangent themselves and two given lines. "Draw…