Archimedies Principle
"It is evident that, when a solid is immersed in a fluid, it will displace exactly its own volume of…
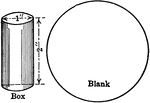
Cylindrical Box - Blank
Sheet metal blank for making a cylindrical box with a diameter of 1 inch and a height of 2 inches.

Capacity
"To find the number of bushels of grain in a bin or box, multiply the length in feet by the height in…

Vertical Cross Section of Spherical Zones of a Casting
An illustration of a vertical cross section of the spherical zones of a casting with a diameter of 16…
Combinational Volume
"Suppose our volume of hydrogen to unite with the volume of chlorine; if one particle of hydrogen combines…
Combinational Volume
"When one volume of hydrogen actually unites with one volume of chlorine, two volumes and not one volume…
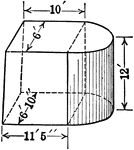
Composite Figure of Quadrilateral Frustum With Half of a Cylinder Attached
An illustration of a composite figure made up of a quadrilateral frustum and half of a cylinder. Frustum…

Cross Section of Concrete Conduit
Cross section of concrete conduit. The diagram can be used to find volume.
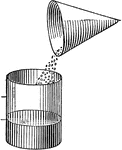
Comparative Volumes Of A Cone And Cylinder
Illustration used to compare the volumes of a cone and a cylinder by emptying sand from the cone into…
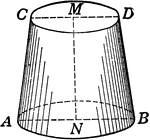
Circular Cone Frustum
An illustration of a circular cone with the top cut off by a plane parallel to the base. The remaining…

Frustum of Cone to Find Volume
"The volume of a frustum of a circular cone is equivalent to the sum of the volumes of three cones whose…
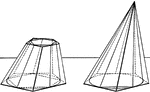
Cone With Regular Polygon Inscribed and Circumscribed About
Illustration of a pyramid and with a regular polygon inscribed in and circumscribed about a cone. "If…
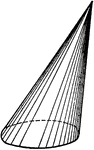
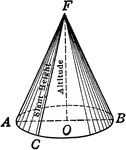
Right Circular Cone
An illustration of a right circular cone with labels on slant height and altitude.

Right Circular Cone
An illustration of a right circular cone with labels on slant height (12.422), radius (8), and altitude…
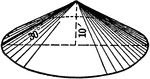
Right Circular Cone 10 Feet High With 30 Degree Angle
An illustration of a right circular cone with altitude of 10 ft. and angle of 30 degrees.

Right Circular Cone With 2 ft. Height and 1 ft. Radius
An illustration of a right circular cone with la radius of 1 foot and a height of 2 feet. Illustration…
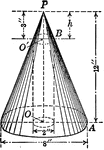
Right Circular Cone With Hole Cut Out
An illustration of a right circular cone with labels on dimensions, and hole cut out. Illustration could…

Comparative Volumes Of A Cone, Sphere, And Cylinder
Illustration used to compare the volumes of a cone, a sphere, and a cylinder.

Volume of Cone
Illustration of a cone with a polygon inscribed used to show that the volume of a circular cone is equal…

Cube for Illustrating Volume
An illustration of a cube divided into 6 equal pyramids to illustrate how volume can be found.
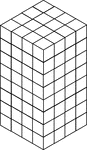
128 Stacked Congruent Cubes
Illustration of 128 congruent cubes stacked so they form a rectangular solid that measures 4 by 4 by…
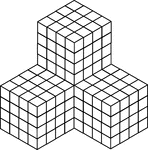
256 Stacked Congruent Cubes
Illustration of 256 congruent cubes stacked so they form 4 larger cubes that measures 4 by 4 by 4 each.…

27 Stacked Congruent Cubes
Illustration of 27 congruent cubes stacked to resemble a larger cube that measures three by three by…
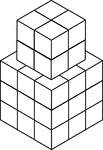
35 Stacked Congruent Cubes
Illustration of 35 congruent cubes stacked at various heights. A 3-dimensional representation on a 2-dimensional…

36 Stacked Congruent Cubes
Illustration of 36 congruent cubes stacked to resemble a 1 by 1 by 1 cube on a 2 by 2 by 2 cube on a…
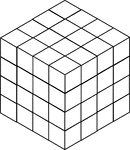
64 Stacked Congruent Cubes
Illustration of 64 congruent cubes stacked so they form a cube that measures 4 by 4 by 4. A 3-dimensional…
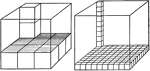
Comparison Of Units Of Cubic Measure
Illustration comparing the fundamental units of measure 1 cubic yard and 1 cubic meter.
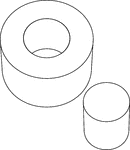
Cylinder Cut From a Cylinder
Illustration of a right circular cylinder with a smaller cylinder removed from the center and placed…
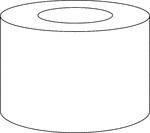
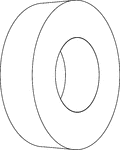
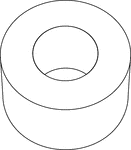
Hollow Cylinder
Illustration of a thin hollow cylinder. It resembles a washer and is often referred to as a disc.
Narrow Cylinder on Side
Illustration of a narrow right circular cylinder (with the height much smaller than the diameter) resting…
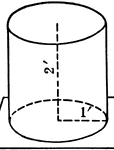
Right Circular Cylinder With 1 ft. Radius and 2 ft. height.
Right circular cylinder with a radius of 1 foot and a height/altitude of 2 feet.

2 Narrow Cylinders on Their Sides
Illustration of 2 narrow right circular cylinders with equal heights (thickness) and different diameters.…
2 Similar Cylinders
Illustration of 2 similar cylinders. The height and diameter of the smaller cylinder is half that of…
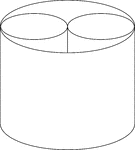
2 Smaller Cylinders In A Larger Cylinder
A large cylinder containing 2 smaller congruent cylinders. The small cylinders are externally tangent…

2 Soup Can Cylinders
Illustration of 2 soup cans that are similar cylinders. The diameter and height of the smaller can is…
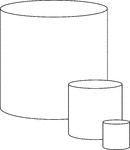
3 Similar Cylinders
Illustration of 3 similar cylinders. The height and diameter in each successively smaller cylinder is…
3 Similar Cylinders
Illustration of 3 similar cylinders. The height and diameter in each successively smaller cylinder is…
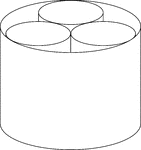
3 Smaller Cylinders In A Larger Cylinder
A large cylinder containing 3 smaller congruent cylinders. The small cylinders are externally tangent…
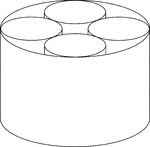
4 Smaller Cylinders In A Larger Cylinder
A large cylinder containing 4 smaller congruent cylinders. The small cylinders are externally tangent…
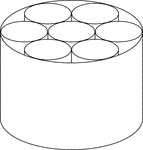
7 Smaller Cylinders In A Larger Cylinder
A large cylinder containing 7 smaller congruent cylinders. The small cylinders are externally tangent…

Book With Decorative Divider
A decorative divider that resembles a book with bookmarks dangling on each side.
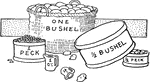
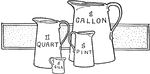
Dry Measures
Containers of dry measure in comparison: one bushel, peck, one half bushel, and one half peck. Illustration…
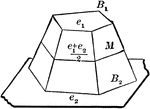
Volume of Frustum of a Pyramid
Diagram used to prove the theorem: "The volume of the frustum of a pyramid (cone) is equal to the sum…

Nicholson Hydrometer
"The Nicholson hydrometer of constant volume is a hollow cylinder carrying at its lower end a basket,…
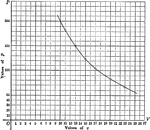
Logarithmic Graph of the Law of Expansion
Logarithmic graph (smooth curve) modeling the law of expansion with values of volume and pressure.
Parallelopiped Showing Volume
Illustration of a parallelopiped (a prism with a parallelogram as its base) used to demonstrate that…
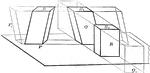
Volume of Parallelopiped
Diagram used to prove the theorem: "The volume of a any parallelopiped is equal to the product of its…
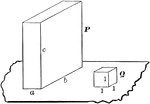
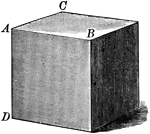
Volume of Rectangular Parallelopiped
Diagram used to prove the theorem: "The volume of a rectangular parallelopiped is equal to the product…