Lit2Go

Almost contemporaneously with the publication in 1637 of Descartes' geometry, the principles of the integral calculus, so far as they are concerned with summation, were being worked out in Italy. This was effected by what was called the principle of indivisibles, and was the invention of Cavalieri. It was applied by him and his contemporaries to numerous problems connected with the quadrature of curves and surfaces, the determination on volumes, and the positions of centres of mass. It served the same purpose as the tedious method of exhaustions used by the Greeks; in principle the methods are the same, but the notation of indivisibles is more concise and convenient. It was, in its turn, superceded at the beginning of the eighteenth century by the integral calculus.

Bonaventura Cavalieri was born at Milan in 1598, and died at Bologna on November 27, 1647. He became a Jesuit at an early age; on the recommendation of the Order he was in 1629 made professor of mathematics at Bologna; and he continued to occupy the chair there until his death. I have already mentioned Cavalieri's name in connection with the introduction of the use of logarithms into Italy, and have alluded to his discovery of the expression for the area of a spherical triangle in terms of the spherical excess. He was one of the most influential mathematicians of his time, but his subsequent reputation rests mainly on his invention of the principle of indivisibles.

The principle of indivisibles had been used by Kepler in 1604 and 1615 in a somewhat crude form. It was first stated by Cavalieri in 1629, but he did not publish his results till 1635. In his early enunciation of the principle in 1635 Cavalieri asserted that a line was made up of an infinite number of points (each without magnitude), a surface of infinite number of lines (each without breadth), and a volume of an infinite number of surfaces (each without thickness). To meet the objections of Guldinus and others, the statement was recast, and in its final form as used by the mathematicians of the seventeenth century it was published in Cavalieri's Exercitationes Geometricae in 1647; the third exercise is devoted to a defence of the theory. This book contains the earliest demonstration of the properties of Pappus. Cavalieri's works on indivisibles were reissued with his later corrections in 1653.

The method of indivisibles rests, in effect, on the assumption that any magnitude may be divided into an infinite number of small quantities which can be made to bear any required ratios (ex. gr. equality) one to the other. The analysis given by Cavalieri is hardly worth quoting except as being one of the first steps taken towards the formation of an infinitesimal calculus. One example will suffice. Suppose it be required to find the area of a right-angled triangle. Let the base be made up of, or contain n points (or indivisibles), and similarly let the other side contain na points, then the ordinates at the successive points of the base will contain a, 2a ..., na points. Therefore the number of points in the area is a + 2a + ... + na; the sum of which is 1/2 n²a + 1/2na. Since n is very large, we may neglect 1/2na for it is inconsiderable compared with 1/2n²a. Hence the area is equal to 1/2(na)n, that is, 1/2 x altitude x base. There is no difficulty in criticizing such a proof, but, although the form in which it is presented is indefensible, the substance of it is correct.

It would be misleading to give the above as the only specimen of the method of indivisibles, and I therefore quote another example, taken from a later writer, which will fairly illustrate the use of the method when modified and corrected by the method of limits.

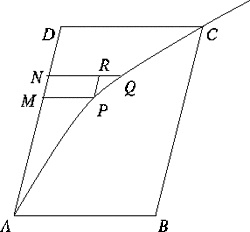
Let it be required to find the area outside a parabola APC and bounded by the curve, the tangent at A, and a line DC parallel to AB the diameter at A. Complete the parallelogram ABCD. Divide AD into n equal parts, let AM contain r of them, and let MN be the (r + 1)th part. Draw MP and NQ parallel to AB, and draw PR parallel to AD. Then when n becomes indefinitely large, the curvilinear area APCD will be the the limit of the sum of all parallelograms like PN. Now

area PN : area BD = MP.MN : DC.AD.

But by the properties of the parabola

MP : DC = AM² : AD² = r² : n²,

and MN : AD = 1 : n. Hence MP.MN : DC.AD = r² : n³. Therefore area PN : area BD = r² : n³. Therefore, ultimately,

area APCD : area BD = 1² + 2² + ... + (n-1)² : n³
                                    = 1/6 n (n-1)(2n-1) : n³

which, in the limit, = 1 : 3.

It is perhaps worth noticing that Cavalieri and his successors always used the method to find the ratio of two areas, volumes, or magnitudes of the same kind and dimensions, that is, they never thought of an area as containing so many units of area. The idea of comparing a magnitude with a unit of the same kind seems to have been due to Wallis.

It is evident that in its direct form the method is applicable to only a few curves. Cavalieri proved that, if m be a positive integer, then the limit, when n is infinite, of (1^m + 2^m + ... + n^m)/n^m+1 is 1/(m+1), which is equivalent to saying that he found the integral of x to x^m from x = 0 to x = 1; he also discussed the quadrature of the hyperbola.