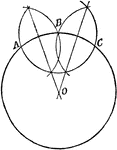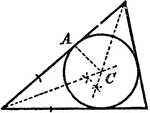
Construction Of The Center And Radius Of A Circle Tangent To Triangle Sides
An illustration showing how to construct a center and radius of a circle that will tangent the three…
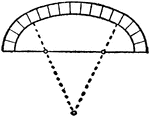
Center Arch
"Three center arches, employed in French Flamboyant." — The Encyclopedia Britannica, 1910
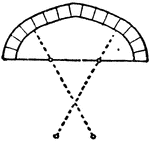
Center Arch
"Four center arches, employed in the Perpendicular and Tudor periods." — The Encyclopedia Britannica,…

Center of Gravity
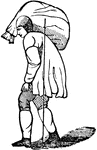
"Why does a person carrying a weight upon his back stoop forward? In order to bring the center of gravity…
Center of Gravity
"Why does a person carrying a weight upon his back stoop forward? In order to bring the center of gravity…
Center of Gravity
"The center of gravity, in any body or system of bodies is that point upon which the body, or system…
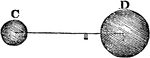
Center of Gravity
"But if one of the balls be heavier than the other, then the centre of gravity will, in proportion,…

Center of Gravity
"In a body of equal thickness, as a board, or a slab of marble, but otherwise of an irregular shape,…

Center of Gravity
"If w and W, fig. 3, be two bodies of known weight, their center of gravity will be at C." —Hallock…
!["The part of the body in which the centre of gravity is situated, may be found, in some cases, by balancing it on a point. Thus the centre of gravity of the poker represented [here] lies directly over the point on which it is balanced." —Quackenbos 1859](https://etc.usf.edu/clipart/36300/36326/centergrav_36326_mth.gif)
Center of Gravity
"The part of the body in which the centre of gravity is situated, may be found, in some cases, by balancing…
Center of Gravity
"When such a surface is irregular in shape, suspend it at any point, so that it may move freely, and…

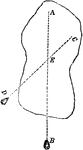
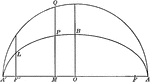
Center of Gravity of Standing Blocks
"Where five blocks are placed in this position, the point of gravity is near the centre of the thrd…
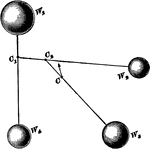
Compound Center of Gravity
"Find the center of gravity of two of the bodies, as W1, and W4, in fig 4. Assume that the weight of…
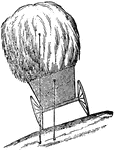
Center of Gravity of a Load of Hay
"A load of hay...upsets where one wheel rises by little above the other, because it is broader on the…
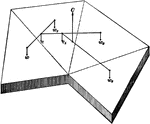
Center of Gravity of an Irregular Plane
"To find the center of gravity of any irregular plane figure, but of uniform thickness throughout, divide…
!["When a line of direction falls within the base, a body stands when not, it falls... On the same principle, a load of stone may pass safely over a hillside, on which a load of hay would be overturned [as shown by the line of direction in this illustration]." —Quackenbos 1859](https://etc.usf.edu/clipart/36300/36329/lod_cog_36329_mth.gif)
Line of Direction from the Center of Gravity of an Object
"When a line of direction falls within the base, a body stands when not, it falls... On the same principle,…
!["When two bodies of equal weight are connected by a rod, the centre of gravity will lie in the middle of that rod. When two bodies of unequal weight are so connected, the centre of gravity will be nearer to the heavier one. These principles are illustrated [here], in which C represents the centre of gravity." —Quackenbos 1859](https://etc.usf.edu/clipart/36300/36328/cog_rod_36328_mth.gif)
Center of Gravity of Rod with Weights
"When two bodies of equal weight are connected by a rod, the centre of gravity will lie in the middle…
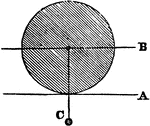
Center of Gravity of a Rolling Ball
"When a ball is rolling on a horizontal plane, the centre of gravity is not raised, but moves in a straight…
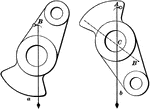
Center of Gravity of a Solid
"In a body free to move, the center of gravity will lie in a vertical plumb-line drawn through the point…
Center of Inertia
"But, suppose the same bar or iron, whose inertia was overcome by raising the centre, to have balls…
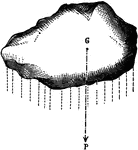
Center of Mass
"A body's center of mass is the point about which all matter composing the body may be balanced. It…
Finding the Center of Mass
"Let any irregularly shpaed body, as a stone or chair, be suspended so as to move freely. Drop a plumb…
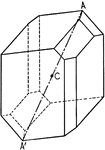
Symmetry center
"A crystal has a center of symmetry if an imaginary line is passed from some point on its surface through…
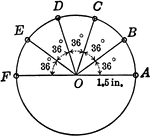
Circle With 36 degree Angles and Radius 1.5 in.
Circle with 36 degree angles marked. This diagram can be used with the following trig problem: Locate…
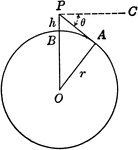
Circle With Center o and Radius r with point P
Circle modeling the earth. O is the center of the earth, r the radius of the earth, and h the height…
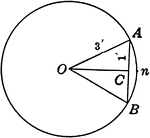
Circle With a Chord of 2 ft. and a Radius of 3 ft.
Circle with chord AB=2 ft. and radius OA = 3 ft.. Triangle AOC is a right triangle. Angle AOC=half angle…

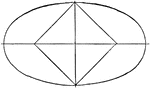
Square Circumscribed About A Circle
Illustration of a square, with diagonals drawn, circumscribed about a circle. This can also be described…

Square Circumscribed About A Circle
Illustration of a square, with 1 diagonals drawn, circumscribed about a circle. This can also be described…

Square Circumscribed About A Circle
Illustration of a square circumscribed about a circle. This can also be described as a circle inscribed…

Square Inscribed In A Circle
Illustration of a square, with diagonals drawn, inscribed in a circle. This can also be described as…
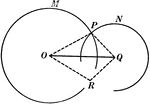
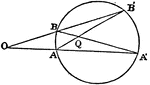
Circumferences of 2 Circles
Illustration used to prove "If two circumferences meet at a point which is not on their line of centers,…

Market Cross
A market cross is a structure used to mark a market square in market towns, originally from Western…
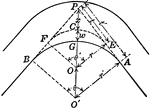
Curve in Pavement of Road
Illustration of blueprint used by highway engineers to widen the pavement on the inside of the curve…

Diurnal Parallax
"If we suppose a spectator placed at G, in the Earth's center, he would see the moon E, among the stars…
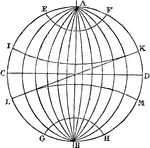
Earth Divisions
"The Earth, whose diameter is 7,912 miles, is represented by the globe, or sphere. The straight line…
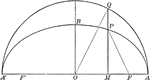
Corresponding Points in an Ellipse and Circle
Illustration of half of an ellipse. "The ordinates of two corresponding points in an ellipse and its…
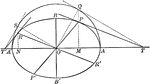
Conjugate Diameters of an Ellipse
Illustration showing that if one diameter is conjugate to a second, the second is conjugate to the first.

Construction of an Ellipse
Illustration of half of an ellipse and its auxiliary circle used to construct an ellipse by points,…
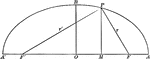
Focal Radii of an Ellipse
Illustration of half of an ellipse. "If d denotes the abscissa of a point of an ellipse, r and r' its…
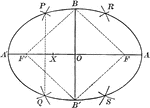
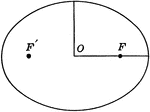
Ellipse With Parts Labeled
Illustration of an ellipse with foci F' and F, major axis A' to A, minor axis B' to B, and center O.
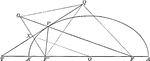
Line Bisecting Angle Between Focal Radii on Ellipse
Illustration of half of an ellipse. "If through a point P of an ellipse a line is drawn bisecting the…
Ordinate and Major Axis of Ellipse
Illustration of half of an ellipse. The square of the ordinate of a point in an ellipse is to the product…
Parallel Tangents to an Ellipse
Illustration showing that tangents drawn at the ends of any diameter are parallel to each other.
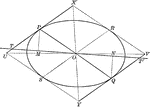
Parts of Ellipse
Diagram of an ellipse that can used to illustrate the different parts. Segment MN is the major axis,…
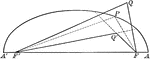
Point Distances to Foci on Ellipse
Illustration of half of an ellipse. "The sum of the distances of any point from the foci of an ellipse…
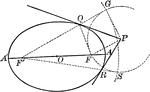
Tangent From External Point to an Ellipse
Illustration of how to draw a tangent to an ellipse from an external point.

Tangents to an Ellipse
Illustration showing the tangents drawn at two corresponding points of an ellipse and its auxiliary…

Construction Of An Equilateral Triangle Inscribed In A Circle
An illustration showing how to construct an equilateral triangle inscribed in a circle. "With the radius…
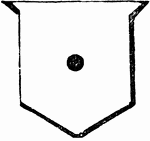
Fess Point
"FESS POINT. The exact centre of the escutcheon, as seen in the annexed example." -Hall, 1862
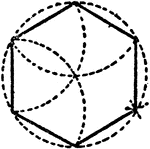
Construction Of A Hexagon In A Circle
An illustration showing how to construct a hexagon in a given circle. "The radius of the circle is equal…
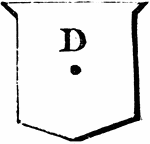
Honour Point
"HONOUR POINT. That part of the shield between the precise middle chief and the fess point. In the annexed…
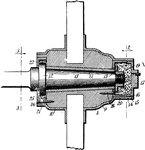
Wheel Hub
The central part of a car wheel (or fan or propeller etc) through which the shaft or axle passes
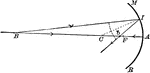
Rays Diverging from Beyond the Center of Curvature on a Concave Mirror
"When the rays diverge from a point beyond the center of curvature, as B, the focus falls on the same…
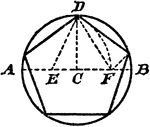
Construction Of A Pentagon Inscribed In A Circle
An illustration showing how to construct a pentagon inscribed in a circle. "Draw the diameter AB, and…
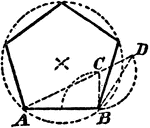
Construction Of A Pentagon On A Line
An illustration showing how to construct a pentagon on a given line. "From B erect BC perpendicular…