Clipart tagged: ‘proof’
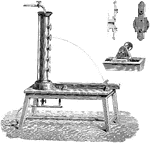
Apparatus for verifying Torricelli's Theorem
This figure represents an apparatus frequently employed for illustrating some of the consequences of…
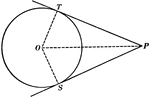
Equal Tangents to Circle Theorem
Illustration used to show that "If two tangents are drawn from any given point to a circle, those tangents…
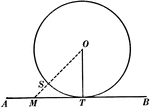
Tangent to Perpendicular Radius Circle Theorem
Illustration used to show that "A tangent to a circle is perpendicular to the radius drawn to the point…
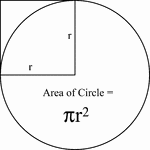
Area Of A Circle
An illustration used to show how the area of a circle is calculated. Area is equal to the product of…
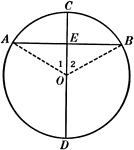
Diameter Perpendicular to a Chord in a Circle
Illustration used to show that "The diameter perpendicular to a chord bisects the chord and also its…
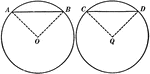
Equal Chords in Equal Circles Theorem
Illustration used to show that "In equal circles, or in the same circle, if two chords are equal, they…
Equal Chords in Equal Circles Theorem
Illustration used to show that "In equal circles, or in the same circle, if two chords are equal, they…

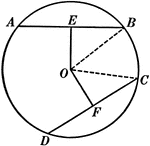
Unequal Chords in Circles Theorem
Illustration used to show that "In equal circles, or in the same circle, if two chords are unequal,…
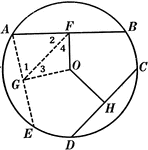
Unequal Chords in Equal Circles Theorem
Illustration used to show that "In equal circles, or in the same circle, if two chords are unequal,…
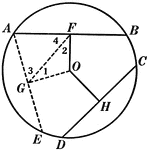
Unequal Chords in Equal Circles Theorem
Illustration used to show that "In equal circles, or in the same circle, if two chords are unequal,…
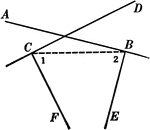
Intersecting Lines Corollary
Illustration used to prove the corollary that "Two lines perpendicular respectively to two intersecting…
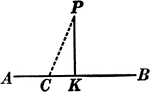
Perpendicular to Line Corollary
Illustration used to prove the corollary that "From a point outside a line there exists only one perpendicular…
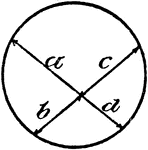
Model Of Geometric Proportions In A Circle
An illustration showing a model of a circle with intersecting chords that illustrates the following…
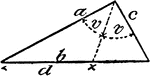
Model Of Geometric Proportions In A Triangle
An illustration showing a model of a triangle that illustrates the following relationship: a:c = d:(b…
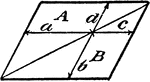
Model Of Geometric Proportions
An illustration showing a quadrilateral model that illustrates the following relationships: a:b = c:d,…
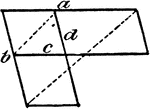
Model Of Geometric Proportions
An illustration showing a model that illustrates the following relationships: a:b = c:d, ad = bc. Product…
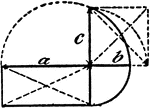
Model Of Geometric Proportions
An illustration showing a model that illustrates the following relationships: a:b = c:b, ab = c²,…
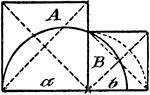
Model Of Geometric Proportions
An illustration showing a model that illustrates the following relationship: A:B = a:b.
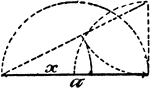
Model Of Geometric Proportions
An illustration showing a model that illustrates the following relationships: a:x = x:a - x, x = √(a²…
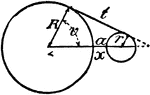
Model Of Geometric Relationships In 2 Circles
An illustration showing a model of 2 circles with tangent lines, diameters, and radii that illustrates…
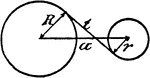
Model Of Geometric Relationships In 2 Circles
An illustration showing a model of 2 circles with tangent lines, diameters, and radii that illustrates…
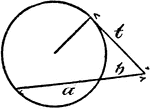
Model Of Geometric Relationships In A Circle
An illustration showing a model of a circle with an exterior angle formed between a tangent and a secant…
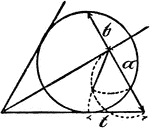
Model Of Geometric Relationships In A Circle
An illustration showing a model of a circle with angles formed between tangents and secants that illustrates…
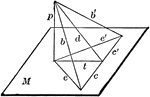
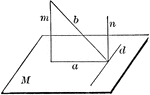
Perpendicular To Line In Plane
"If from the foot of a perpendicular to a plane a straight line is drawn at right angles to any line…
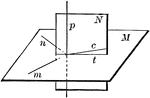
Plane Perpendicular To Line
"All the perpendiculars to a straight line at the same point lie in a plane perpendicular to the line."
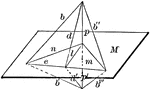
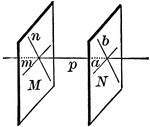
Line Perpendicular To Plane
"If a straight line is perpendicular to each of two straight lines at their point of intersection it…
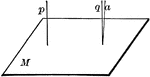
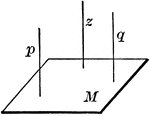
Lines Perpendicular To A Plane
"If one of two parallels is perpendicular to a plane, the other is also."
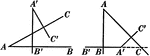
Angles With Perpendicular Sides Are Equal or Supplementary Proof
Illustration used to prove "Two angles whose sides are perpendicular each to each are either equal or…

Euclid's Pythagorean Theorem Proof
Illustration used to prove the Pythagorean Theorem, according to Euclid. A perpendicular is drawn from…

Exterior Angle Proof
Illustration used to prove "An exterior angle of a triangle is equal to the sum of the two remote interior…

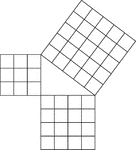
Geometric Pythagorean Theorem Proof
Illustration that can be used to prove the Pythagorean Theorem, the sum of the squares of the legs is…
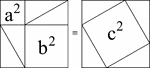
Geometric Pythagorean Theorem Proof
Illustration that can be used to prove the Pythagorean Theorem, the sum of the squares of the legs is…
Pythagorean Theorem Proof by Rearrangement
A visual illustration used to prove the Pythagorean Theorem by rearrangement. When the 4 identical triangles…
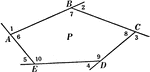
Sum of Exterior Angles of a Polygon Proof
Illustration used to prove "If the sides of any polygon are prolonged in succession one way, no two…
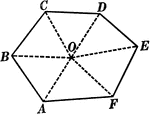
Sum of Interior Angles of a Polygon Proof
Illustration used to prove "The sum of all the angles of any polygon is twice as many right angles as…

Hand with Proof-plane
"A proof-plane may be made by cementing a bronze cent or a disk of gilt paper to a thin insulating handle,…
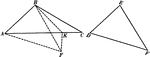
2 Triangles Theorem
Illustration used to prove that "If two triangles have two sides of one equal respectively to two sides…
2 Triangles Theorem
Illustration used to prove that "If two triangles have two sides of one equal respectively to two sides…
Exterior Angle of Triangle Theorem
Illustration used to prove that "If one side of a triangle is prolonged, the exterior angle formed is…
Parallel Lines Theorem
Illustration used to prove that "If two straight lines are parallel to a third straight line, they are…
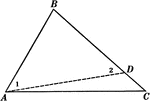
Sides of Triangle Theorem
Illustration used to prove that "If two sides of a triangle are unequal, the angle opposite the greater…
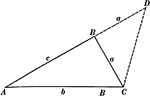
Sides of Triangle Theorem
Illustration used to prove that "The sum of any two sides of a triangle is greater than the third side."
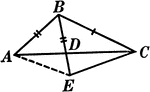
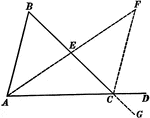
Segments Labeled In A Triangle
Illustration of triangle ABC with BE extended through the triangle at point D. Segment AB is equal to…