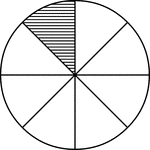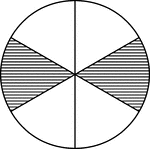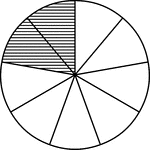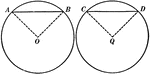
Equal Chords in Equal Circles Theorem
Illustration used to show that "In equal circles, or in the same circle, if two chords are equal, they…
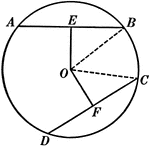
Unequal Chords in Circles Theorem
Illustration used to show that "In equal circles, or in the same circle, if two chords are unequal,…
Diameter Perpendicular to a Chord in a Circle
Illustration used to show that "The diameter perpendicular to a chord bisects the chord and also its…
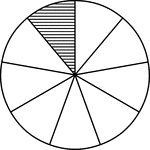
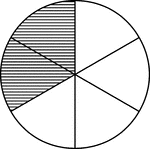
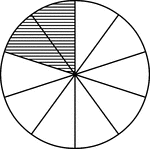
Equal Chords in Equal Circles Theorem
Illustration used to show that "In equal circles, or in the same circle, if two chords are equal, they…
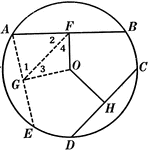
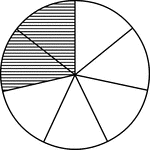
Unequal Chords in Equal Circles Theorem
Illustration used to show that "In equal circles, or in the same circle, if two chords are unequal,…
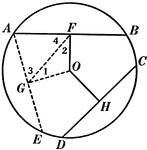
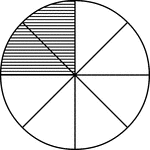
Unequal Chords in Equal Circles Theorem
Illustration used to show that "In equal circles, or in the same circle, if two chords are unequal,…
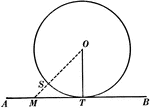
Tangent to Perpendicular Radius Circle Theorem
Illustration used to show that "A tangent to a circle is perpendicular to the radius drawn to the point…
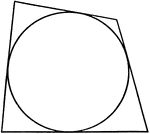
Quadrilateral Circumscribed About a Circle
Illustration of a quadrilateral circumscribed about a circle. This could also be described as a circle…
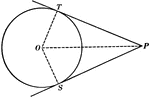
Equal Tangents to Circle Theorem
Illustration used to show that "If two tangents are drawn from any given point to a circle, those tangents…
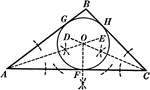
Construction Used to Inscribe a Circle in a Triangle
Illustration used to inscribe a circle in a given triangle.
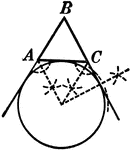
Construction Used to Escribe a Circle to a Triangle
Illustration used to escribe a circle to a given triangle. "A circle which is tangent to one side of…
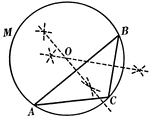
Construction Used to Circumscribe a Circle About a Triangle
Illustration used to circumscribe a circle about a given triangle.
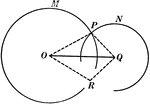
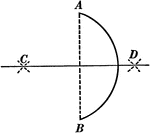
Circumferences of 2 Circles
Illustration used to prove "If two circumferences meet at a point which is not on their line of centers,…
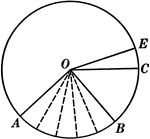
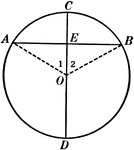
Central Angles and Arcs in a Circle
Illustration of a circle that can be used to show that an "angle at the center of a circle is measured…
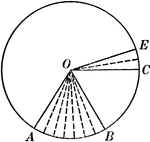
Central Angles and Arcs in a Circle
Illustration of a circle that can be used to show that an "angle at the center of a circle is measured…
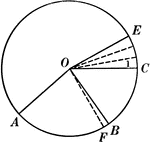
Central Angles and Arcs in a Circle
Illustration of a circle that can be used to show that an "angle at the center of a circle is measured…
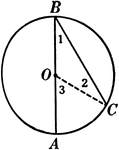
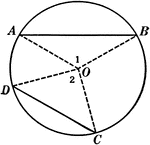
Inscribed Angle in a Circle Proof
Illustration of a circle with an inscribed angle that can be used to prove that "An inscribed angle…
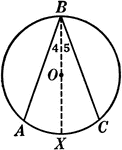
Inscribed Angle in a Circle Proof
Illustration of a circle with an inscribed angle that can be used to prove that "An inscribed angle…
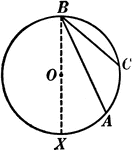
Inscribed Angle in a Circle Proof
Illustration of a circle with an inscribed angle that can be used to prove that "An inscribed angle…
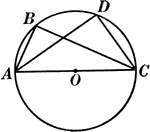
Angles Inscribed in the Same Segment Circle Proof
Illustration of a circle used to prove "All angles inscribed in the same segment are equal."
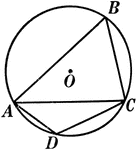
Right Angles Inscribed in Semicircle Proof
Illustration of a circle used to prove "Any angle inscribed in a semicircle is a right angle."
Obtuse Angles Inscribed in Circle Proof
Illustration of a circle used to prove "Any angle inscribed in a segment less than a semicircle is an…
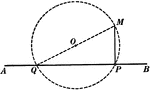
Construction of a Tangent to a Circle
Illustration used to show how "to construct a tangent to a circle from a point outside."
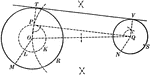
Construction of an External Tangent to 2 Circles
Illustration used to show how "to construct a common external tangent to two given circles."
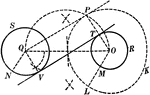
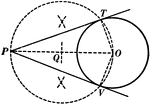
Construction of an 2 External Tangents to 2 Circles
Illustration used to show how to construct two common external tangents to two given circles.

Elves and Fairies Dancing
According to Norse mythology, in Elfland, elves and fairies would dance in a circle in the moonlight.…
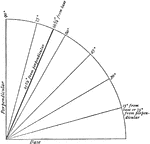
Inclination of Earth's Axis
"A quadrant, or one fourth of a circle. The oblique lines indicate various angles with the base. The…

Byzantine Capital
"Byzantine Capital. The leading forms of the Byzantine style are the round arch, the circle, and in…

Derby Flycatcher
"Pitangus derbianus. Derby Flycatcher. Under parts light wood-brown, with an olive tinge; wings and…

Crested Auk in Winter
"Simorhynchus cristatellus. Crested Auk. Snub-nosed Auk. A beautiful crest of 12-20 slender feathers…

Eurasian Sparrowhawk Muscles
"Muscles of a bird (accipiter nisus), after Carus, Tab. Anat. Comp., 1828, pl. 4. a, pharynx; b, trachea;…