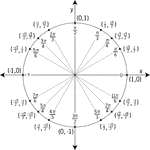
Unit Circle Labeled With Special Angles And Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
Unit Circle Labeled At Special Angles
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…

Unit Circle Labeled At Special Angles
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
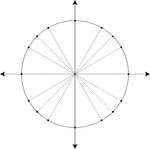
Unit Circle Marked At Special Angles
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane. All…
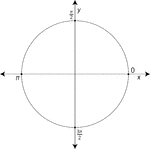
Unit Circle Labeled At Quadrantal Angles
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
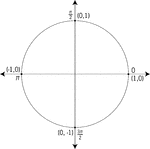
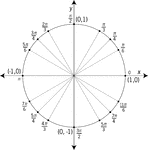
Unit Circle Labeled With Quadrantal Angles And Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane. All…
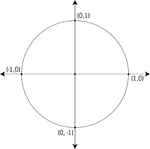
Unit Circle Labeled With Quadrantal Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane. At each…
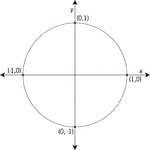
Unit Circle Labeled With Quadrantal Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
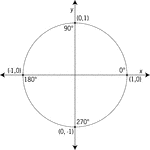
Unit Circle Labeled With Quadrantal Angles And Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
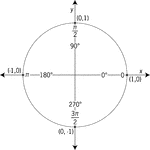
Unit Circle Labeled With Quadrantal Angles And Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
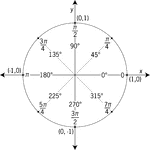
Unit Circle Labeled In 45° Increments With Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
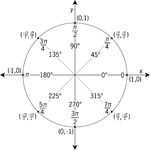
Unit Circle Labeled In 45° Increments With Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
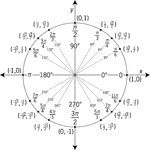
Unit Circle Labeled With Special Angles And Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
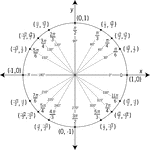
Unit Circle Labeled With Special Angles And Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
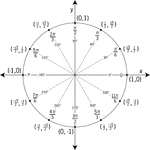
Unit Circle Labeled In 30° Increments With Values
Illustration of a unit circle (circle with a radius of 1) superimposed on the coordinate plane with…
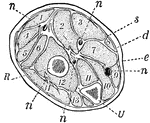
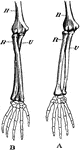
Forearm, Section of
A section across the forearm a short distance below the elbow-joint. R and U, its two supporting bones,…
Bones of the Arm
Bones of the arm. Labels: A, arm in supination; B, arm in pronation. H, humerus; R, radius; U, ulna.
Bow Pencil
Bow compasses should be used on all arcs and circles having a radius of less than 3/4 inch.
Bow Divider
Bow compasses should be used on all arcs and circles having a radius of less than 3/4 inch.

Beam Compasses
For larger circles beam compasses are used. The two parts called channels which carry the pen and the…
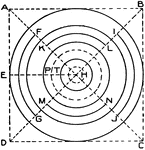
Circle Exercise
Circle pattern exercise: Draw diagonals A C and D B, and with the T-square draw the line E H. Now mark…

Arteries of the Hand and Forearm
Arteries of the palm of the head and front of the forearm. Labels: 3, deep part of the raised pronator…
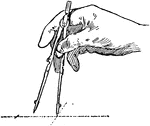
Adjusting the Compass
In changing the compass from a small to large radius, hold the legs together with one hand and spin…
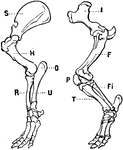
Tapir Legs
"Fore and Hind Leg of a Tapir. A, scapula; I, ilium, or shinbone of pelvis; H, humerus; F, femur; O,…
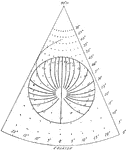
Diurnal Cotidal Lines
This figure shows "the cotidal lines and lines of equal amplitude for a diurnal tide in a circular sea…
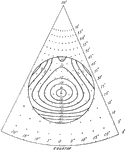
Diurnal Cotidal Lines
This figure shows "the cotidal lines and lines of equal amplitude for a diurnal tide in a circular sea…
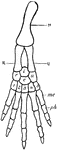
Vertebrate Fore Limb
"Ideal fore limb. H., Humerus; R., radius; U., ulna; r'., radiale; u'., ulnare; i., intermedium; c.,…
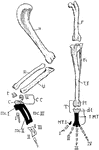
Bird Limbs
"Fore-limb and hind-limb compared. H., Humerus; R., radius; U., ulna; r., radiale; u., ulnare; C., distal…

Dove Wing
"Wing of dove. h., Humerus; s.f., secondary feathers; r., radius; u., ulna; c., carpals; mc., carpo-metacarpus;…
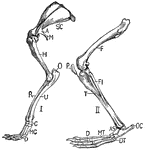
Rabbit Limbs
"Fore-limb and shoulder-girdle (I.) and hind-limb (II.) of rabbit. SC., Scapula; A., acromion; M., metacromion…
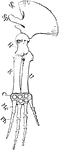
Whale Forelimb
"Left fore-limb of Balaenoptera. Sc., Sca pula with spine (sp.); H., humerus; R., radius; U., ulna;…

Gorilla Skeleton
"Skeleton of male gorilla. cl., Clavicle; sc., tip of scapula; S., praesternum; H., humerus; r., radius;…
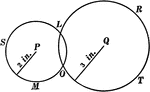
2 Intersecting Circles
Illustration showing a circle with a radius of 2 in. intersecting a circle with a radius of 3 in..
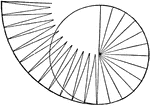
Circle Made Up Of Triangles
"A circle may be considered as made up of triangles whose bases form the circumference, and whose altitude…
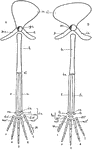
Vertebrate Appendages
"Diagrams of the girdles and appendages in a typical Vertebrate. A, anterior; B, posterior. ac., acetabulum,…
Crocodile Skeleton
"Skeleton of crocodile. C, causal region; D, thoracic region of spinal column; F, fibula; Fe, femur;…
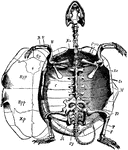
Marsh Turtle Skeleton
"Cistudo lutaria. Skeleton seen from below; the plastron has been removed and is represented on one…
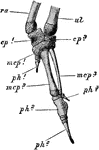
Rock Pigeon Manus
"Columba livia. Left manus of a nestling. The cartilaginous parts are dotted. cp. 1, radiale; cp. 2,…

Circle Parts
A circle with labels for radius, diameter, and circumference. The visual will help to remember what…
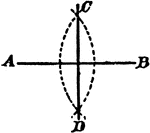
Construction Of A Line Divided In Equal Parts
An illustration showing the construction used to divide a line AB into two equal parts; and to erect…
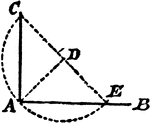
Construction Of A Perpendicular
An illustration showing the construction used to erect a perpendicular at the end of a line. "With the…
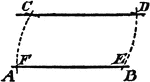
Construction Of A Parallel
An illustration showing the construction used to erect a parallel line. "With C as a center, draw the…
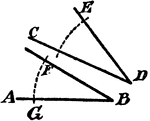
Construction Of An Equal Angle
An illustration showing the construction used to erect an equal angle. "With D as a center, draw the…
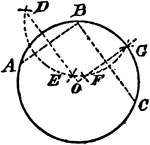
Find The Center Of A Circle Through 3 Points
An illustration showing how to find the center of a circle which will pass through three given points…
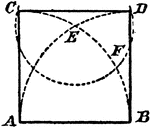
Square Constructed Upon A Given Line
An illustration showing how to construct a square upon a given line. "With AB as radius and A and B…
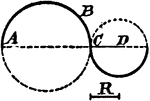
Construction Of Circle Tangent To Circle
An illustration showing how to construct a tangent circle to a circle with a given radius. "Through…
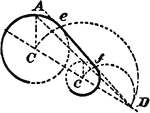
Construction Of Tangent To 2 Circles
An illustration showing how to construct a tangent to 2 given circles of different diameters. "Join…
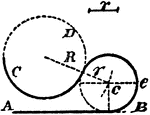
Construction Of A Circle Tangent To A Line And A Circle
An illustration showing how to construct a circle tangent to a given line and given circle. "Add the…
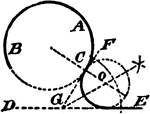
Construction Of A Center And Radius Of A Circle That Will Tangent A Given Circle
An illustration showing how to construct the center and radius of a circle that will tangent a given…
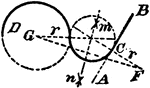
Construction Of A Center And Radius Of A Circle That Will Tangent A Given Circle And Line
An illustration showing how to construct the center and radius of a circle that will tangent a given…
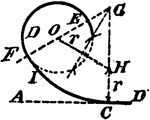
Construction Of A Center And Radius Of A Circle That Will Tangent A Given Circle And Line
An illustration showing how to construct the center and radius of a circle that will tangent a given…
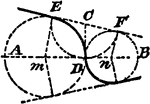
Construction Of Two Circles That Tangent Themselves and 2 Given Lines
An illustration showing how to construct two circles that tangent themselves and two given lines. "Draw…
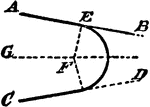
Construction Of A Circle That Tangents 2 Given Lines
An illustration showing how to construct a circle that tangents two given lines inclined to one another…
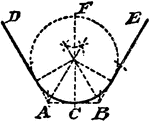
Construction Of A Circle That Tangents 2 Given Lines And Goes Through A Given Point
An illustration showing how to construct a circle that tangents two given lines and goes through a given…
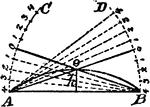
Construction Of A Circle Arc
An illustration showing how to construct a circle arc without recourse to its center, but its chord…
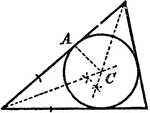
Construction Of The Center And Radius Of A Circle Tangent To Triangle Sides
An illustration showing how to construct a center and radius of a circle that will tangent the three…

Construction Of An Equilateral Triangle Inscribed In A Circle
An illustration showing how to construct an equilateral triangle inscribed in a circle. "With the radius…