Trigonometry Grid With Domain -2π to 2π And Range -10 to 10
Illustration of a trigonometric grid with a domain from -2π to 2π and a range from -10 to 10.…
Trigonometry Grid With Domain -3π to 3π And Range -1 to 1
Illustration of a trigonometric grid with a domain from -3π to 3π and a range from -1 to 1. The…
Trigonometry Grid With Domain -3π to 3π And Range -2 to 2
Illustration of a trigonometric grid with a domain from -3π to 3π and a range from -2 to 2. The…

Trigonometry Grid With Domain -3π to 3π And Range -3 to 3
Illustration of a trigonometric grid with a domain from -3π to 3π and a range from -3 to 3. The…
Trigonometry Grid With Domain -3π to 3π And Range -4 to 4
Illustration of a trigonometric grid with a domain from -3π to 3π and a range from -4 to 4. The…
Trigonometry Grid With Domain -3π to 3π And Range -5 to 5
Illustration of a trigonometric grid with a domain from -3π to 3π and a range from -5 to 5. The…
Trigonometry Grid With Domain -3π to 3π And Range -6 to 6
Illustration of a trigonometric grid with a domain from -3π to 3π and a range from -6 to 6. The…

Trigonometry Grid With Domain -3π to 3π And Range -7 to 7
Illustration of a trigonometric grid with a domain from -3π to 3π and a range from -7 to 7. The…

Trigonometry Grid With Domain -3π to 3π And Range -8 to 8
Illustration of a trigonometric grid with a domain from -3π to 3π and a range from -8 to 8. The…
Trigonometry Grid With Domain -3π to 3π And Range -9 to 9
Illustration of a trigonometric grid with a domain from -3π to 3π and a range from -9 to 9. The…
Trigonometry Grid With Domain -3π to 3π And Range -10 to 10
Illustration of a trigonometric grid with a domain from -3π to 3π and a range from -10 to 10.…
Trigonometry Grid With Domain -4π to 4π And Range -2 to 2
Illustration of a trigonometric grid with a domain from -4π to 4π and a range from -2 to 2. The…
Trigonometry Grid With Domain -4π to 4π And Range -3 to 3
Illustration of a trigonometric grid with a domain from -4π to 4π and a range from -3 to 3. The…

Trigonometry Grid With Domain -4π to 4π And Range -4 to 4
Illustration of a trigonometric grid with a domain from -4π to 4π and a range from -4 to 4. The…

Trigonometry Grid With Domain -4π to 4π And Range -5 to 5
Illustration of a trigonometric grid with a domain from -4π to 4π and a range from -5 to 5. The…
Trigonometry Grid With Domain -4π to 4π And Range -6 to 6
Illustration of a trigonometric grid with a domain from -4π to 4π and a range from -6 to 6. The…

Trigonometry Grid With Domain -4π to 4π And Range -7 to 7
Illustration of a trigonometric grid with a domain from -4π to 4π and a range from -7 to 7. The…
Trigonometry Grid With Domain -4π to 4π And Range -8 to 8
Illustration of a trigonometric grid with a domain from -4π to 4π and a range from -8 to 8. The…

Trigonometry Grid With Domain -4π to 4π And Range -9 to 9
Illustration of a trigonometric grid with a domain from -4π to 4π and a range from -9 to 9. The…
Trigonometry Grid With Domain -4π to 4π And Range -10 to 10
Illustration of a trigonometric grid with a domain from -4π to 4π and a range from -10 to 10.…

Stylolites
Two of the interlocking prisms or stylolites, showing the striated sides produced by friction during…
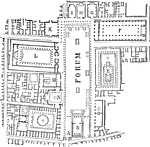
Forum of Pompeii
"Forum of Pompeii. A, principal entrance; B, a Corinthian temple; C, the public prison (carcer publicus);…

Lateral Area of A Prism
Diagram used to prove the theorem: "The lateral area of a prism is equal to the product of a lateral…
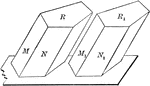
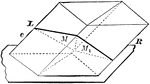
Two Equal Prisms
Diagram used to prove the theorem: "Two prisms are equal when the three faces about a trihedral of one…
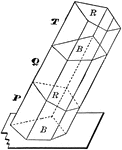
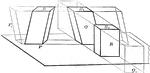
Oblique Prism Truncated Into 3 Sections
Illustration of an oblique prism constructed by the combination of three truncated prisms.
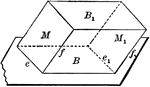
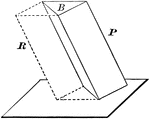
Equal and Parallel Opposite Faces of a Parallelopiped
Diagram used to prove the theorem: "The opposite faces of a parallelopiped are equal and parallel."
Parallelopiped Divided Into Triangular Prisms
Diagram used to prove the theorem: "The plane passed through two diagonally opposite edges of a parallelopiped…
Relationship Between 2 Parallelopipeds With Equal Altitudes
Diagram used to prove the theorem: "The rectangular parallelopipeds which have two dimensions in common…

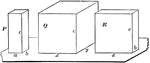
Relationship Between Dimensions of Parallelopipeds
Diagram used to prove the theorem: "The rectangular parallelopipeds are to each other as the product…
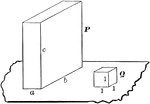
Volume of Rectangular Parallelopiped
Diagram used to prove the theorem: "The volume of a rectangular parallelopiped is equal to the product…
Volume of Parallelopiped
Diagram used to prove the theorem: "The volume of a any parallelopiped is equal to the product of its…
Volume of Triangular Prism
Diagram used to prove the theorem: "The volume of a triangular prism is equal to the product of its…

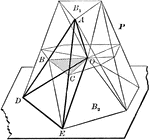
Volume of Triangular Pyramid
Diagram used to prove the theorem: "The volume of a triangular pyramid is equal to one third of a triangular…
Volume of Prismatoid
Diagram used to prove the theorem: "The volume of a prismatoid is equal to the product of one-sixth…
Lozenge Ordinary
"Argent, a lozenge, vert. The lozenge is formed by four equal and parallel lines but not rectangular,…

Arkansaw Goldfinch
"Astragalinus psaltria. Arkansaw Goldfinch. Upper parts uniform olive-green, without any black; below…
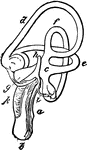
The Inner Ear of an Eagle
"Membranous labyrinth of Haliaetus albicilla (White-tailed Eagle), X2. a,b, cochlea; b, its saccular…
The Inner Ear of a White-tailed Eagle
"Membranous labyrinth of Haliaetus albicilla (White-tailed Eagle), X2. a,b, cochlea; b, its saccular…

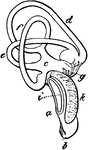
A Section of an Eagle's Cochlea
"Section of the cochlea, X3. a, vestibular surface of external cartilaginous prism, extending into d,…
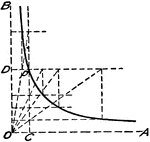
Drawing Rectangular Hyperbola
"Let OA and OB be the asymptotes and P a point on the curve. Draw PC and PD. Mark any points on Pc;…
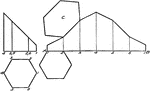
Development of Hexagonal Prism
An illustration of a hexagonal prism rolled out, or "stretched out" in the straight line AB.

Development of Rectangular Pyramid
The illustration of a rectangular pyramid unfolded by creating edges equal length to the base and meeting…

Triangle Prism Exercise
An illustration to draw triangle prism's development, or stretched out surfaces, in a 4" by 5" surface.
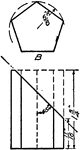
Pentagon Development Prism Exercise
An exercise developed to draw a rolled out or development of the pentagon prism in a 4" by 5" surface.
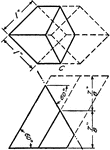
Pentagonal Prism Development Exercise
An exercise in drawing a pentagonal prism development or rolled out image in a 4" by 5" area.
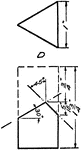
Triangular Prism Development Exercise
An illustration to exercise a stretched out, or development, image of the triangular prism using 4"…
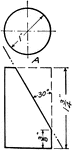
Development Exercise of Cylinder
An exercise problem in creating a development or rolled out surface of a cylinder in a 4" by 5" drawing…
Development Exercise of Cylinder using Three Piece Elbow
The exercise problem of creating a three piece elbow development or rolled out image of the cylinder…
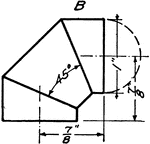
Development Exercise of Octagonal Roof and True Shape of Rafter
Problem exercise in drawing a development or a stretchout image of the octagonal roof and finding the…
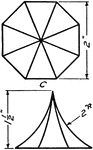
Development Exercise of Dome and True Shape of Hip
A development or rolled out image exercise problem of the dome and finding the true shape of the hip,…
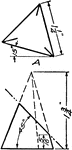
Development Exercise of Triangular Pyramid
Exercise problem to develop, or rolled out, image of the triangular pyramid by creating an equal length…
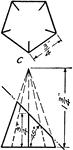
Development Exercise of Pentagonal Pyramid
A pentagonal pyramid problem exercise to complete the top view of the image, and development, or rolled…
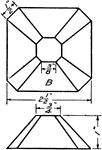
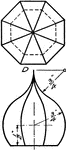
Development Exercise of Octagonal Light Shade
A problem exercise creating a stretched out or developed image of the octagonal light shade by using…
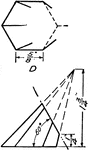
Development Exercise of Hexagonal Pyramid
A sample exercise problem in completing the top part of the hexagonal pyramid and to create a development,…
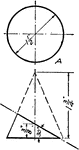
Development Exercise of Cone
Development and top completion exercise problem of the cone by dividing the base into equal parts and…
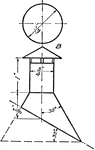
Development Exercise of Flange and Hood Cones
An exercise problem to complete the top and develop, stretched out, image of the flange and hood cones…
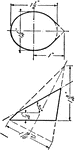
Development Exercise of Pentagonal Pyramid
The problem exercise in completing the top view and creating the development, or rolled out, image of…
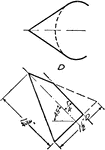
Development Exercise of Oblique Hexagonal Pyramid
A sample exercise problem to complete the top part and create a stretched out image of the oblique hexagonal…
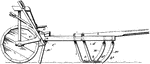
Land Leveler
This specification discloses a land leveler comprising a massive rectangular frame including reinforced…

Rectangular Trunk Trimming
This chest is one of the oldest forms of furniture. It is a rectangular structure with four walls and…