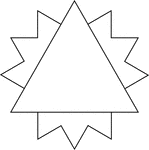
Triangle Inscribed In A 12-Point Star
Illustration of an equilateral triangle inscribed in a closed concave geometric figure with 24 sides…

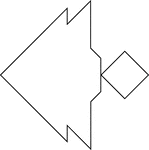
Angelfish
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…
Angelfish
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…

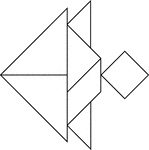
Angelfish
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…
Angelfish
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…
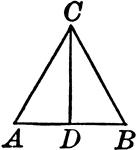
Bisected Vertical Angle of an Isosceles Triangle
Illustration to show that the bisector of the vertical angle of an isosceles triangle bisects the base,…
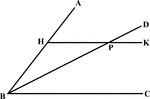
Angle Bisector Drawn Parallel to A Side
Illustration to show that if through any point in the bisector of an angle a line is drawn parallel…
Angles Used to Illustrate Sum and Difference of Two Angles
Angles used to illustrate the sum and difference of two angles and trig identities.
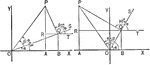
Sum of 2 Acute Angles
Illustration of two triangles, showing the sine of the sum of two acute angles expressed in terms of…
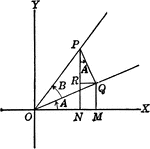
Reference Angles/Triangles Formed by Angles in Quadrants
Lines drawn to horizontal to form triangle ratios (reference triangles, angles).
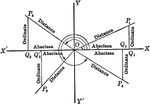
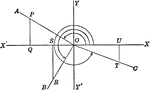
Reference Angles/Triangles Formed by Angles in Quadrants With Labels
Lines drawn to horizontal to form triangle ratios (reference triangles, angles). Axes, quadrants, abscissa,…
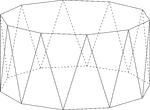
Decagonal Antiprism
Illustration of a decagonal antiprism. An antiprism is formed by having two parallel congruent bases…
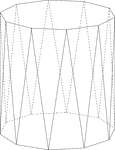
Decagonal Antiprism
Illustration of a decagonal antiprism. An antiprism is formed by having two parallel congruent bases…

Dodecagonal Antiprism
Illustration of a dodecagonal antiprism. An antiprism is formed by having two parallel congruent bases…
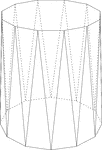
Dodecagonal Antiprism
Illustration of a dodecagonal antiprism. An antiprism is formed by having two parallel congruent bases…
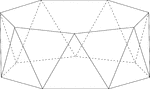
Heptagonal/Septagonal Antiprism
Illustration of a heptagonal, or sometimes known as a septagonal antiprism. An antiprism is formed by…

Heptagonal/Septagonal Antiprism
Illustration of a heptagonal, or sometimes known as a septagonal antiprism. An antiprism is formed by…

Hexagonal Antiprism
Illustration of a hexagonal antiprism. An antiprism is formed by having two parallel congruent bases…
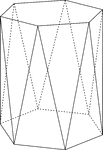
Hexagonal Antiprism
Illustration of a hexagonal antiprism. An antiprism is formed by having two parallel congruent bases…
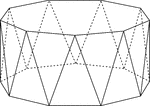
Nonagonal Antiprism
Illustration of a nonagonal antiprism. An antiprism is formed by having two parallel congruent bases…

Nonagonal Antiprism
Illustration of a nonagonal antiprism. An antiprism is formed by having two parallel congruent bases…
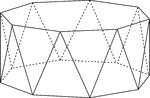
Octagonal Antiprism
Illustration of an octagonal antiprism. An antiprism is formed by having two parallel congruent bases…
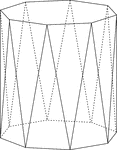
Octagonal Antiprism
Illustration of an octagonal antiprism. An antiprism is formed by having two parallel congruent bases…
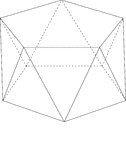
Pentagonal Antiprism
Illustration of a pentagonal antiprism. An antiprism is formed by having two parallel congruent bases…
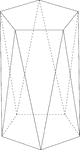
Pentagonal Antiprism
Illustration of a pentagonal antiprism. An antiprism is formed by having two parallel congruent bases…
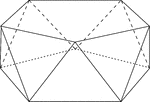
Pentagonal Antiprism
Illustration of a pentagonal antiprism. An antiprism is formed by having two parallel congruent bases…
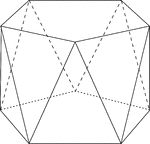
Pentagonal Antiprism
Illustration of a pentagonal antiprism. An antiprism is formed by having two parallel congruent bases…
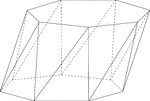
Skewed Heptagonal/Septagonal Antiprism
Illustration of a skewed (non-right) heptagonal, or sometimes known as a septagonal antiprism. An antiprism…
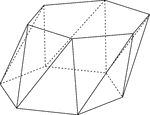
Skewed Hexagonal Antiprism
Illustration of a skewed (non-right) hexagonal antiprism. An antiprism is formed by having two parallel…
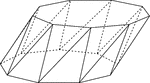
Skewed Nonagonal Antiprism
Illustration of a skewed (non-right) nonagonal antiprism. An antiprism is formed by having two parallel…
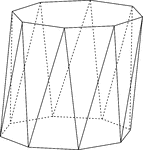
Skewed Octagonal Antiprism
Illustration of a skewed (non-right) octagonal antiprism. An antiprism is formed by having two parallel…
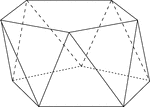
Skewed Pentagonal Antiprism
Illustration of a skewed (non-right) pentagonal antiprism. An antiprism is formed by having two parallel…
Arch
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…
Arch
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…
Arch
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…
Arch
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…
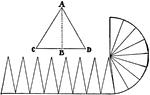
Area of Circle with Triangles
"In the triangle above, the line AB is its altitude. Since we know how to find the area of one triangle,…

Arrow Pointing Left
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…
Arrow Pointing Left
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…
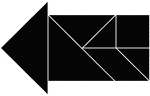
Arrow Pointing Left
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…
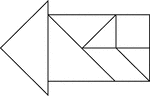
Arrow Pointing Left
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…

Bear
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…

Bear
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…

Bear
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…
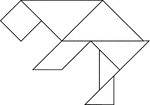
Bear
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…

Bearded Man in a Tophat
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…
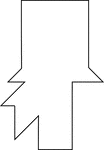
Bearded Man in a Tophat
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…

Bearded Man in Tophat
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…
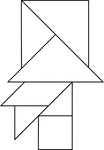
Bearded Man in Tophat
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…

Beta Fish
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…
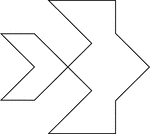
Beta Fish
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…

Beta Fish
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…
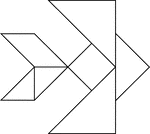
Beta Fish
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…
Boat
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…
Boat
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…
Boat
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…
Boat
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…

Camel
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…
Camel
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…

Camel
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…