Camel
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…

Cat
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…
Cat
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…

Cat
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…
Cat
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…
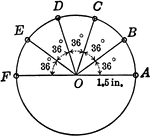
Circle With 36 degree Angles and Radius 1.5 in.
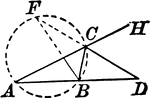
Circle with 36 degree angles marked. This diagram can be used with the following trig problem: Locate…
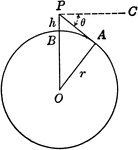
Circle With Center o and Radius r with point P
Circle modeling the earth. O is the center of the earth, r the radius of the earth, and h the height…
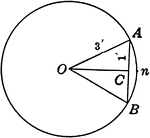
Circle With a Chord of 2 ft. and a Radius of 3 ft.
Circle with chord AB=2 ft. and radius OA = 3 ft.. Triangle AOC is a right triangle. Angle AOC=half angle…
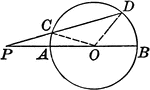
Circle With Diameter, Radius, Segment, Line
Illustration showing a circle with a diameter, radius, lines, triangle, and segment drawn.
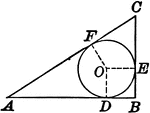
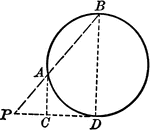
Circle Inscribed in a Right Triangle
Illustration showing the diameter of a circle inscribed in a right triangle is equal to the difference…
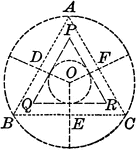
Circle With Triangles and Circle Within
Illustration showing a circle with equilateral triangles and another circle within.
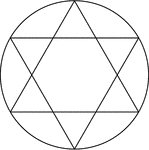
Star Inscribed In A Circle
Illustration of a 6-point star created by two equilateral triangles (often described as the Star of…
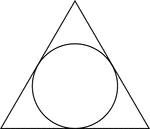
Triangle Circumscribed About A Circle
Illustration of an equilateral triangle circumscribed about a circle. This can also be described as…

Triangle Inscribed in Circle
Illustration of triangle inscribed in circle. Or, circle circumscribed about triangle.
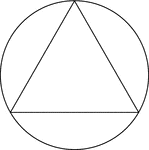
Triangle Inscribed In A Circle
Illustration of an equilateral triangle inscribed in a circle. This can also be described as a circle…

Triangles Making Up A Circle
Illustration showing that a circle may be considered as made up of triangles whose bases form the circumference.

Circle With Inscribed Equilateral Triangle
Illustration showing an equilateral triangle inscribed in a circle.

Circle With Inscribed Quadrilateral and Triangles Formed
Illustration showing a circle with an inscribed quadrilateral and triangles formed by extended chords.
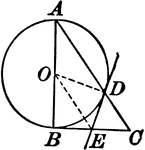
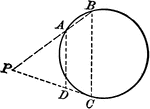
Circle With a Right Triangle
Illustration where one leg of a right triangle is the diameter of a circle. The tangent at the point…
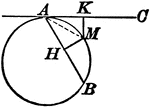
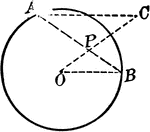
Circle With a Tangent Line and Chord
Illustration showing that from any point in the circumference of a circle, a chord and a tangent are…

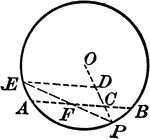
Two Intersecting Circles With Lines
Illustration showing 2 intersecting circles with a lines drawn that form a triangle.

Triangle With Circle Constructions
Illustration of a triangle with its incircle and three excircles constructed.

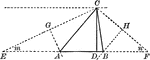
Construction to Circumscribe a Circle About a Triangle
Illustration of the construction used to circumscribe a circle about a given triangle.
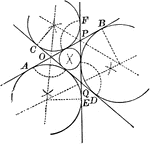
Construction of Escribed Circles With Ex-centres
Illustration of the construction used to escribe circles with centres (centers) called ex-centres of…
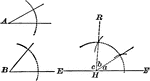
Construction to Find the Third Angle of a Triangle When Given Two Angles
Illustration of the construction used to find the third angle of a triangle when two of the angles are…
Construction to Inscribe a Circle in a Triangle
Illustration of the construction used to inscribe a circle in a given triangle.
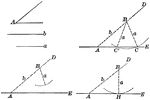
Construction of a Triangle When Given Two Sides and the Angle Opposite (Ambiguous Case)
Illustration of the construction used to make a triangle when given two sides and the angle opposite…
Construction of a Triangle When Given Two Sides and the Angle Opposite (Ambiguous Case)
Illustration of the construction used to make a triangle when given two sides and the angle opposite…

Construction of a Triangle When Given Two Sides and the Angle Opposite (Ambiguous Case)
Illustration of the construction used to make a triangle when given two sides and the angle opposite…
Construction of a Triangle Given Perimeter, Angle, Altitude
Illustration used to construct a triangle , given the perimeter, one angle, and the altitude from the…
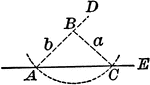
Construction of a Triangle When Given a Side and Two Angles
Illustration of the construction used to make a triangle when given a side and two angles.
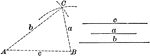
Construction of a Triangle When Given Three Sides
Illustration of the construction used to make a triangle when given three sides.
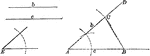
Construction of a Triangle When Given Two Sides and Included Angle
Illustration of the construction used to make a triangle when given two sides and the included angle.
Positioning Pen for Constructions
Illustration showing the correct and incorrect position of a right line pen against a T-square, triangle,…
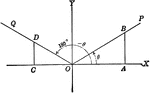
Coordinate Axis With Angles, Lines, and Perpendiculars Drawn
Coordinate axis with angle XOP equal to theta, Θ, and angle XOQ=180 - Θ. From any point in the terminal…

Coordinate Axis With Perpendiculars Drawn To Form Similar Right Triangles From Positive and Negative Theta, Θ
Angle XOP=Θ and angle XOQ=- Θ. From a point in the terminal side of each a perpendicular line is drawn…
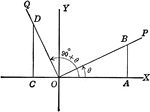
Coordinate Axis With Perpendiculars Drawn To Form Similar Right Triangles
Angle XOP=Θ and angle XOQ=90+Θ. From a point in the terminal side of each a perpendicular line is…

Cormorant
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…
Cormorant
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…

Cormorant
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…
Cormorant
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…

Cup
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…
Cup
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…

Cup
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…
Cup
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…
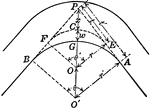
Curve in Pavement of Road
Illustration of blueprint used by highway engineers to widen the pavement on the inside of the curve…

Dancer
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…
Dancer
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…

Dancer
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…
Dancer
Tangrams, invented by the Chinese, are used to develop geometric thinking and spatial sense. Seven figures…
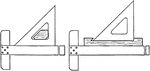
Section Lining Device
A homemade section liner device made by slipping a wooden block to hold the triangle to make cross hatching…