Base Angles In An Isosceles Triangle
Illustration showing that can be used to prove that the base angles of an isosceles triangle are equal.
Equal Segments In An Isosceles Triangle
Illustration showing that if equal segments measured from the end of the base are laid off on the base…
Equal Segments In An Isosceles Triangle
Illustration showing that if equal segments measured from the end of the base prolonged are laid off…
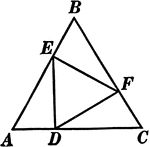
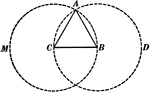
Equilateral Triangle Inscribed In An Equilateral Triangle
Illustration used to prove that triangle EFD is equilateral given that triangle ABC is equilateral and…
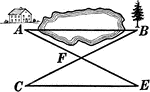
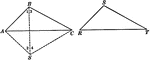
Using Triangles To Measure A Lake
Illustration that uses triangles to measure the distance across a lake.
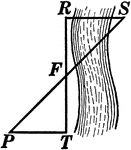
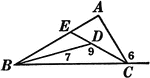
Using Triangles To Measure A River
Illustration that uses triangles to measure the distance across a river.
Using Triangles To Measure A River
Illustration that uses triangles to measure the distance across a river.

Using Triangles To Measure A River
Illustration that uses triangles to measure the distance across a river.
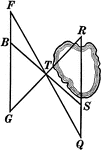
Using Triangles To Measure A Lake
Illustration that uses triangles to measure the distance across a lake.
Equal Triangles
Illustration used to show that two triangles are equal if the three sides of one are equal respectively…
Construction Of Equilateral Triangle
Illustration used to show how to construct an equilateral triangle, with a given line as a side.
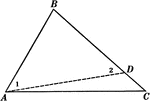
Triangle With Perpendicular Bisector
Illustration showing a perpendicular bisector of a triangle extended outside of the triangle.
Exterior Angle of Triangle Theorem
Illustration used to prove that "If one side of a triangle is prolonged, the exterior angle formed is…
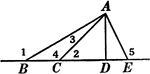
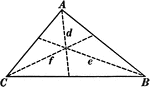
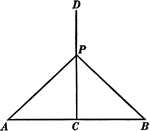
Segments and Angles in a Triangle
Illustration of a triangle with interior segments and angles labeled.
Segments and Angles in a Triangle
Illustration of a triangle with interior segments and angles labeled.
Sides of Triangle Theorem
Illustration used to prove that "If two sides of a triangle are unequal, the angle opposite the greater…
Sides of Triangle Theorem
Illustration used to prove that "The sum of any two sides of a triangle is greater than the third side."
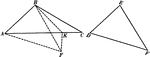
2 Triangles Theorem
Illustration used to prove that "If two triangles have two sides of one equal respectively to two sides…
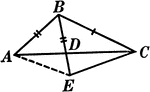
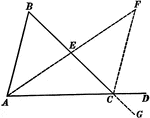
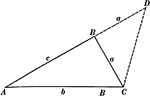
Segments Labeled In A Triangle
Illustration of triangle ABC with BE extended through the triangle at point D. Segment AB is equal to…
2 Triangles Theorem
Illustration used to prove that "If two triangles have two sides of one equal respectively to two sides…
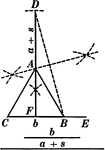
Construction Of An Isosceles Triangle
Illustration of the construction used to create an isosceles triangle, given the bases and the sum of…
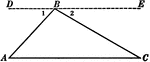
Sum Of Angles In Triangle Theorem
Illustration used to prove the theorem, "The sum of the angles of any triangle is two right angles."
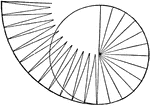
Circle Made Up Of Triangles
"A circle may be considered as made up of triangles whose bases form the circumference, and whose altitude…
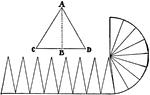
Area of Circle with Triangles
"In the triangle above, the line AB is its altitude. Since we know how to find the area of one triangle,…

Equilateral And Isosceles Triangles
An illustration showing an isosceles triangle in an equilateral triangle.
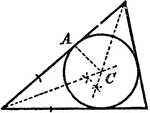
Construction Of The Center And Radius Of A Circle Tangent To Triangle Sides
An illustration showing how to construct a center and radius of a circle that will tangent the three…

Construction Of An Equilateral Triangle Inscribed In A Circle
An illustration showing how to construct an equilateral triangle inscribed in a circle. "With the radius…
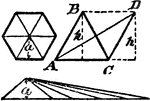
Area Of Regular Polygon Proof
An illustration showing that the area of a regular polygon is equal to the area of a triangle whose…
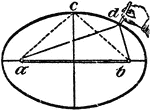
Construction Of An Ellipse
An illustration showing how to construct an ellipse using a string. "Having given the two axes, set…
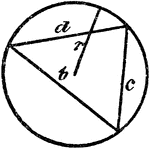
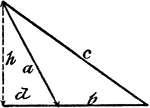
Triangle Inscribed In A Circle
An illustration showing a triangle with sides b, c, and d inscribed in a circle with radius r.
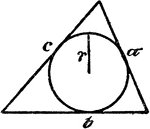
Circle Inscribed In A Triangle
An illustration showing a circle with radius r inscribed in a triangle with sides a, b, and c.
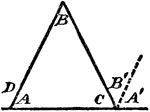
Exterior And Interior Angles Of A Triangle
An illustration showing a triangle with interior angles A, B, C, and exterior angles D, and A' + B'.
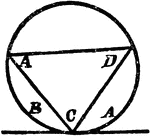
Triangle Inscribed In A Circle
An illustration showing a triangle with angles A, C, and D inscribed in a circle which is tangent to…
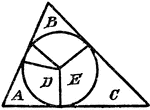
Circle Inscribed In A Triangle
An illustration showing a circle with sectors D and E inscribed in a triangle with angles, A, B, and…
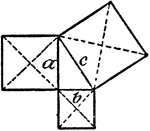
Model Of Pythagorean Theorem
An illustration showing a model that illustrates the Pythagorean Theorem: a² + b² = c².
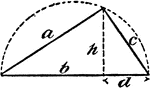
Right Triangle Inscribed In A Semicircle
An illustration of a right triangle inscribed in a semicircle.
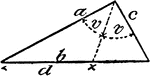
Model Of Geometric Proportions In A Triangle
An illustration showing a model of a triangle that illustrates the following relationship: a:c = d:(b…
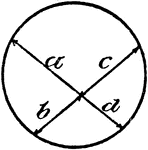
Model Of Geometric Proportions In A Circle
An illustration showing a model of a circle with intersecting chords that illustrates the following…
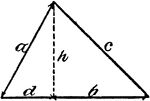
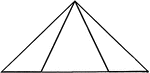
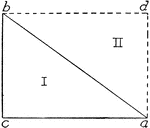
Area of Triangle
"The triangle ABC is divided into 2 right triangles I and II. ABC is seen to be equal to 1/2 of the…
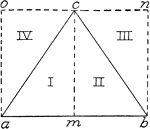
Area of Triangle
"The child sees triangle ACB = triangle ADB, and that I + II = CA - DB; and so he sees that the area…
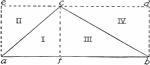
Area of Triangle
"Fig. 3 shows triangle I = triangle II, III = IV, and so triangle ABC = 1/2 of rectangle ABDE. The fact…

Area of Hexagon
Illustration showing how to find the area of a hexagon using the triangles that make it up.
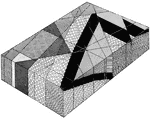
Basalt Diagram
"Diagram to illustrate the inferred structure in the vicinity of the "Triangle." Arkose conglomerate…
Action of Semilunar Valve
Section of the aorta, to show the action of the semilunar valve. A is intended to show the valves, represented…

Tablet Frame
This modern Tablet Architectural frame was in the style of the Italian Renaissance. It had the general…

Pulpit Frame
The pulpit Architectural frame was a German frame that was dated between 1595 to 1597. It had the general…
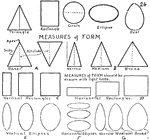
Forms
Showing different types of forms or shapes: rectangle, right triangle, acute triangle, and obtuse triangle.
Shapes
Four different types of forms or shapes: right triangle, isosceles triangle, rectangle, and circle.

Triangles Making Up A Circle
Illustration showing that a circle may be considered as made up of triangles whose bases form the circumference.
Helix
A cylindrical helix is a curve generated by a point moving uniformly around a cylinder and uniformly…

Gravesande's Apparatus
An apparatus for verifying the parallelogram of forces. This method is used in physics for determining…