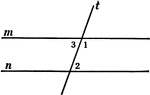
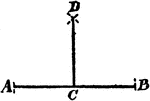
Perpendicular to Line Corollary
Illustration used to prove the corollary that "From a point outside a line there exists only one perpendicular…
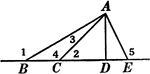
Segments and Angles in a Triangle
Illustration of a triangle with interior segments and angles labeled.
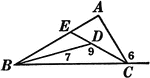
Segments and Angles in a Triangle
Illustration of a triangle with interior segments and angles labeled.
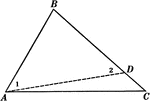
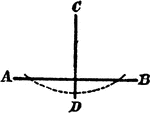
Sides of Triangle Theorem
Illustration used to prove that "If two sides of a triangle are unequal, the angle opposite the greater…
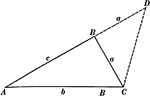
Sides of Triangle Theorem
Illustration used to prove that "The sum of any two sides of a triangle is greater than the third side."
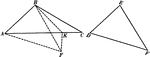
2 Triangles Theorem
Illustration used to prove that "If two triangles have two sides of one equal respectively to two sides…
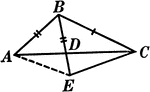
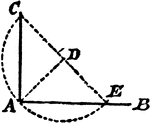
Segments Labeled In A Triangle
Illustration of triangle ABC with BE extended through the triangle at point D. Segment AB is equal to…
2 Triangles Theorem
Illustration used to prove that "If two triangles have two sides of one equal respectively to two sides…
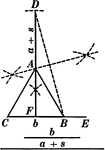
Construction Of An Isosceles Triangle
Illustration of the construction used to create an isosceles triangle, given the bases and the sum of…
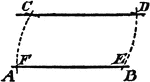
Parallel Lines Theorem
Illustration used to prove that "If two straight lines are parallel to a third straight line, they are…
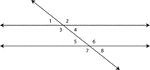
2 Lines Cut By A Transversal
Illustration of two straight lines cut by a transversal. The 8 angles formed are labeled.
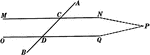
Parallel Lines Cut By A Transversal Theorem
Illustration used to prove the theorem, "If two straight lines are cut by a transversal making a pair…
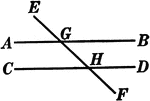
2 Lines Cut By A Transversal
Illustration of two straight lines, AB and CD, cut by a transversal EF.
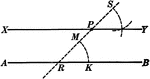
Construction Of A Parallel Line
Illustration of the construction used to create a line parallel to a given line.
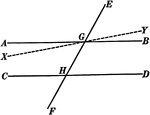
Parallel Lines Cut By A Transversal Theorem
Illustration used to prove the theorem, "If two parallel lines are cut by a transversal, the alternate…
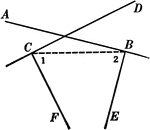
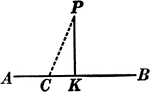
Intersecting Lines Corollary
Illustration used to prove the corollary that "Two lines perpendicular respectively to two intersecting…
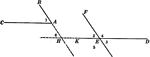
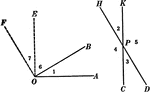
2 Angles With Parallel Sides Theorem
Illustration used to prove the theorem, "Two angles whose sides are parallel, each to each, are either…
2 Angles With Perpendicular Sides Theorem
Illustration used to prove the theorem, "Two angles whose sides are perpendicular, each to each, are…
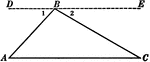
Sum Of Angles In Triangle Theorem
Illustration used to prove the theorem, "The sum of the angles of any triangle is two right angles."

Circle Parts
A circle with labels for radius, diameter, and circumference. The visual will help to remember what…
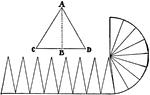
Area of Circle with Triangles
"In the triangle above, the line AB is its altitude. Since we know how to find the area of one triangle,…
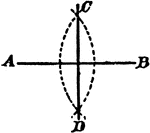
Construction Of A Line Divided In Equal Parts
An illustration showing the construction used to divide a line AB into two equal parts; and to erect…
Construction Of A Perpendicular
An illustration showing the construction used to erect a perpendicular. "With C as a center, draw the…
Construction Of A Perpendicular
An illustration showing the construction used to erect a perpendicular from a point to a line. "With…
Construction Of A Perpendicular
An illustration showing the construction used to erect a perpendicular at the end of a line. "With the…
Construction Of A Parallel
An illustration showing the construction used to erect a parallel line. "With C as a center, draw the…
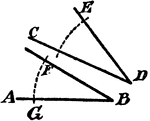
Construction Of An Equal Angle
An illustration showing the construction used to erect an equal angle. "With D as a center, draw the…

Construction Of A Divided Angle
An illustration showing the construction used to divide an angle into two equal parts. "With C as a…
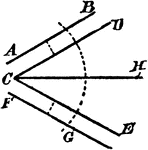
Construction Of A Divided Angle
An illustration showing the construction used to divide an angle into two equal parts when the lines…
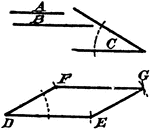
Construction Of A Parallelogram
An illustration showing the construction used to erect a parallelogram given two sides and an angle.…
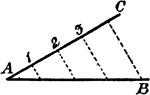
Divide A Line Proportionately
An illustration showing the construction used to divide the line AB in the same proportion of parts…
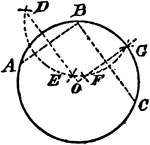
Find The Center Of A Circle Through 3 Points
An illustration showing how to find the center of a circle which will pass through three given points…
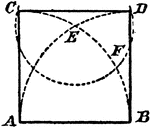
Square Constructed Upon A Given Line
An illustration showing how to construct a square upon a given line. "With AB as radius and A and B…
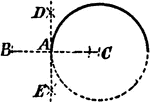
Construction Of Tangent To Circle
An illustration showing how to construct a tangent to a circle through a given point in a circumference.…
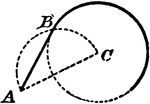
Construction Of Tangent To Circle
An illustration showing how to construct a tangent to a circle through a given point outside of a circumference.…
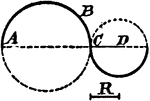
Construction Of Circle Tangent To Circle
An illustration showing how to construct a tangent circle to a circle with a given radius. "Through…
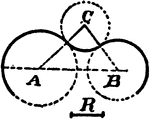
Construction Of Circle Tangent To 2 Circles
An illustration showing how to construct a tangent circle to 2 given circles. "Join centers C and c…
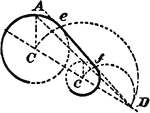
Construction Of Tangent To 2 Circles
An illustration showing how to construct a tangent to 2 given circles of different diameters. "Join…
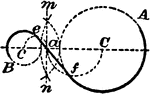
Construction Of Tangent Between 2 Circles
An illustration showing how to construct a tangent between 2 given circles. "Join the centers C and…
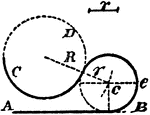
Construction Of A Circle Tangent To A Line And A Circle
An illustration showing how to construct a circle tangent to a given line and given circle. "Add the…
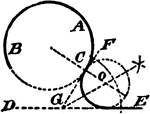
Construction Of A Center And Radius Of A Circle That Will Tangent A Given Circle
An illustration showing how to construct the center and radius of a circle that will tangent a given…
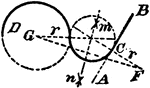
Construction Of A Center And Radius Of A Circle That Will Tangent A Given Circle And Line
An illustration showing how to construct the center and radius of a circle that will tangent a given…
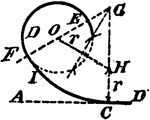
Construction Of A Center And Radius Of A Circle That Will Tangent A Given Circle And Line
An illustration showing how to construct the center and radius of a circle that will tangent a given…
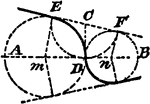
Construction Of Two Circles That Tangent Themselves and 2 Given Lines
An illustration showing how to construct two circles that tangent themselves and two given lines. "Draw…
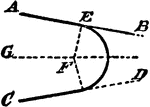
Construction Of A Circle That Tangents 2 Given Lines
An illustration showing how to construct a circle that tangents two given lines inclined to one another…
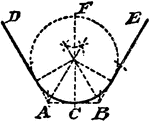
Construction Of A Circle That Tangents 2 Given Lines And Goes Through A Given Point
An illustration showing how to construct a circle that tangents two given lines and goes through a given…
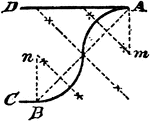
Construction Of A Cyma
An illustration showing how to construct a cyma, or two circle arcs that will tangent themselves, and…
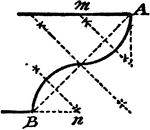
Construction Of A Talon
An illustration showing how to construct a talon, or two circle arcs that will tangent themselves, and…
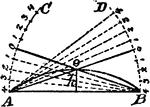
Construction Of A Circle Arc
An illustration showing how to construct a circle arc without recourse to its center, but its chord…
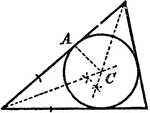
Construction Of The Center And Radius Of A Circle Tangent To Triangle Sides
An illustration showing how to construct a center and radius of a circle that will tangent the three…

Construction Of An Equilateral Triangle Inscribed In A Circle
An illustration showing how to construct an equilateral triangle inscribed in a circle. "With the radius…
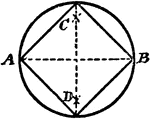
Construction Of A Square Inscribed In A Circle
An illustration showing how to construct a square inscribed in a circle. "Draw the diameter AB, and…

Construction Of A Square Circumscribed About A Circle
An illustration showing how to construct a square circumscribed about a circle. "Draw the diameters…
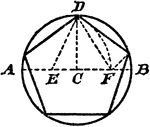
Construction Of A Pentagon Inscribed In A Circle
An illustration showing how to construct a pentagon inscribed in a circle. "Draw the diameter AB, and…
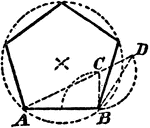
Construction Of A Pentagon On A Line
An illustration showing how to construct a pentagon on a given line. "From B erect BC perpendicular…
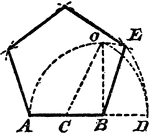
Construction Of A Pentagon On A Line
An illustration showing how to construct a pentagon on a given line without resort to its center. "From…
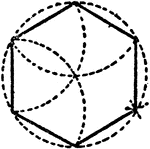
Construction Of A Hexagon In A Circle
An illustration showing how to construct a hexagon in a given circle. "The radius of the circle is equal…
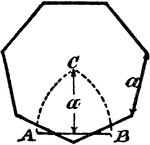
Construction Of A Heptagon
An illustration showing how to construct a heptagon, or septagon. "The appotem a in a hexagon is the…