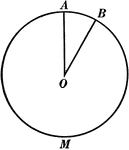
Chords, Diameters, and Radii of a Circle
Illustration of a circle with diameter AB. Radii are RO, SO, AO, and BO. ED is a chord.
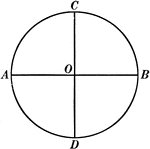
Circle With 2 Perpendicular Diameters
Illustration of a circle with center O and diameters AB and CD perpendicular to each other.
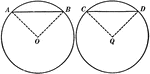
Equal Chords in Equal Circles Theorem
Illustration used to show that "In equal circles, or in the same circle, if two chords are equal, they…

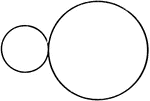
Unequal Chords in Circles Theorem
Illustration used to show that "In equal circles, or in the same circle, if two chords are unequal,…
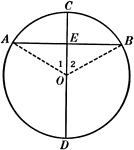
Diameter Perpendicular to a Chord in a Circle
Illustration used to show that "The diameter perpendicular to a chord bisects the chord and also its…
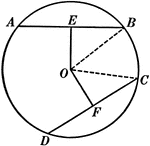
Equal Chords in Equal Circles Theorem
Illustration used to show that "In equal circles, or in the same circle, if two chords are equal, they…
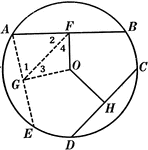
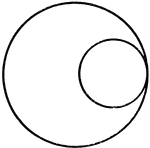
Unequal Chords in Equal Circles Theorem
Illustration used to show that "In equal circles, or in the same circle, if two chords are unequal,…
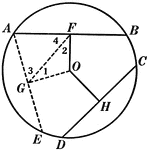
Unequal Chords in Equal Circles Theorem
Illustration used to show that "In equal circles, or in the same circle, if two chords are unequal,…
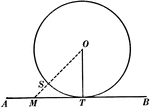
Tangent to Perpendicular Radius Circle Theorem
Illustration used to show that "A tangent to a circle is perpendicular to the radius drawn to the point…
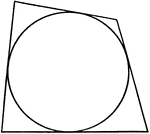
Quadrilateral Circumscribed About a Circle
Illustration of a quadrilateral circumscribed about a circle. This could also be described as a circle…
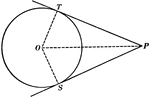
Equal Tangents to Circle Theorem
Illustration used to show that "If two tangents are drawn from any given point to a circle, those tangents…
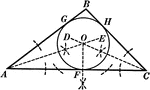
Construction Used to Inscribe a Circle in a Triangle
Illustration used to inscribe a circle in a given triangle.

Construction Used to Escribe a Circle to a Triangle
Illustration used to escribe a circle to a given triangle. "A circle which is tangent to one side of…
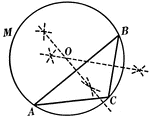
Construction Used to Circumscribe a Circle About a Triangle
Illustration used to circumscribe a circle about a given triangle.
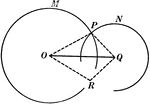
Circumferences of 2 Circles
Illustration used to prove "If two circumferences meet at a point which is not on their line of centers,…
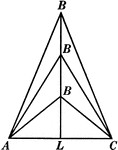
3 Isosceles Triangles Wit Equal Bases
Illustration of three isosceles triangles with the same base AC but varying heights (as B gets farther…

Central Angles and Arcs in a Circle
Illustration of a circle that can be used to show that an "angle at the center of a circle is measured…
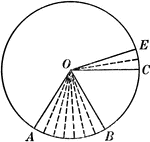
Central Angles and Arcs in a Circle
Illustration of a circle that can be used to show that an "angle at the center of a circle is measured…

Central Angles and Arcs in a Circle
Illustration of a circle that can be used to show that an "angle at the center of a circle is measured…
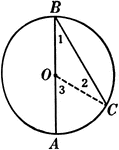
Inscribed Angle in a Circle Proof
Illustration of a circle with an inscribed angle that can be used to prove that "An inscribed angle…
Inscribed Angle in a Circle Proof
Illustration of a circle with an inscribed angle that can be used to prove that "An inscribed angle…
Inscribed Angle in a Circle Proof
Illustration of a circle with an inscribed angle that can be used to prove that "An inscribed angle…
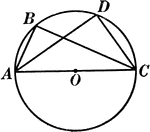
Angles Inscribed in the Same Segment Circle Proof
Illustration of a circle used to prove "All angles inscribed in the same segment are equal."
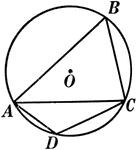
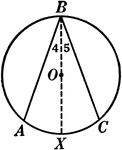
Right Angles Inscribed in Semicircle Proof
Illustration of a circle used to prove "Any angle inscribed in a semicircle is a right angle."
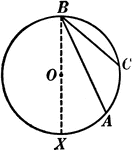
Obtuse Angles Inscribed in Circle Proof
Illustration of a circle used to prove "Any angle inscribed in a segment less than a semicircle is an…
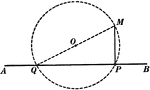
Construction of a Tangent to a Circle
Illustration used to show how "to construct a tangent to a circle from a point outside."
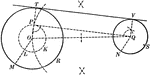
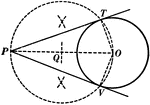
Construction of an External Tangent to 2 Circles
Illustration used to show how "to construct a common external tangent to two given circles."
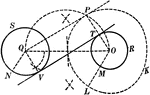
Construction of an 2 External Tangents to 2 Circles
Illustration used to show how to construct two common external tangents to two given circles.
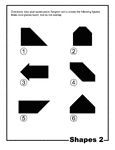
Shapes Silhouette Tangram Card #2
Silhouette outlines of shapes (quadrilateral, hexagon, arrow, pentagon) made from tangram pieces. Tangrams,…
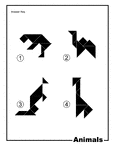
Animals Silhouette Solution Tangram Card
Solutions for silhouette outlines of animals (bear, kangaroo, camel, giraffe) made from tangram pieces.…
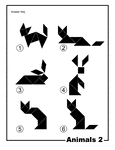
Animals Silhouette Solution Tangram Card #2
Solutions for silhouette outlines of animals (fox, rabbit, cat) made from tangram pieces. Tangrams,…

Birds Silhouette Solution Tangram Card
Solutions for silhouette outlines of birds (duck, swan, turkey vulture, cormorant, and egret) made from…
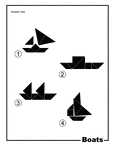
Boats Silhouette Solution Tangram Card
Solutions for silhouette outlines of boats (sailboat, ship, yacht) made from tangram pieces. Tangrams,…

Buildings Silhouette Solution Tangram Card
Solutions for silhouette outlines of buildings (house, lighthouse) made from tangram pieces. Tangrams,…

Fish Silhouette Solution Tangram Card
Solutions for silhouette outlines of fish (shark, parrot fish, angelfish, flounder, hogfish, beta) made…
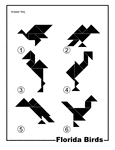
Florida Birds Silhouette Solution Tangram Card
Solutions for silhouette outlines of Florida birds (seagull, mocking bird, egret, flamingo, turkey vulture,…
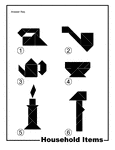
Household Items Silhouette Solution Tangram Card
Solutions for silhouette outlines of household items (iron, pipe, kettle, cup, candle, hammer) made…

People Silhouette Solution Tangram Card
Solutions for silhouette outlines of people (runners) made from tangram pieces. Tangrams, invented by…
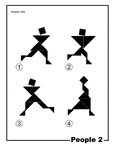
People Silhouette Solution Tangram Card #2
Solutions for silhouette outlines of people (runners, dancers) made from tangram pieces. Tangrams, invented…

People Silhouette Solution Tangram Card #3
Solutions for silhouette outlines of people (woman standing, water skier, woman kneeling, man walking)…
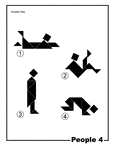
People Silhouette Solution Tangram Card #4
Solutions for silhouette outlines of people (swimmer, reclining man, butler, diver) made from tangram…
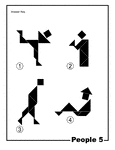
People Silhouette Solution Tangram Card #5
Solutions for silhouette outlines of people (ice skater, saint statue, walking man, reclining man) made…
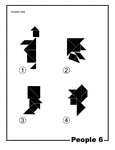
People Silhouette Solution Tangram Card #6
Solutions for silhouette outlines of people (silhouettes of men) made from tangram pieces. Tangrams,…

Sea Animals Silhouette Solution Tangram Card
Solutions for silhouette outlines of sea animals (sea monster, dolphin, sea turtle, stingray) made from…
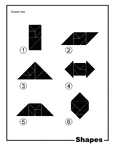
Shapes Silhouette Solution Tangram Card
Solutions for silhouette outlines of shapes (rectangle, parallelogram, isosceles triangle, double arrow,…
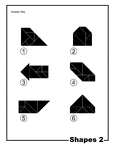
Shapes Silhouette Solution Tangram Card #2
Solutions for silhouette outlines of shapes (quadrilateral, hexagon, arrow, pentagon) made from tangram…

Tangram Pattern, Black with Small Dotted Lines
Tangram pattern with black pieces and thin white-dotted lines. Tangrams, invented by the Chinese, are…

Tangram Pattern, Black with Solid Lines
Tangram pattern with black pieces and thin white-dotted lines. Tangrams, invented by the Chinese, are…

Tangram Pattern, White with Small Dotted Lines
Tangram pattern with black pieces and thin white-dotted lines. Tangrams, invented by the Chinese, are…

Tangram Pattern, White with Solid Lines
Tangram pattern with black pieces and thin white-dotted lines. Tangrams, invented by the Chinese, are…

Tangram Pattern, Black with Small Dotted Lines and Instructions
Tangram pattern with black pieces and thin white-dotted lines. Tangrams, invented by the Chinese, are…

Tangram Pattern, Black with Solid Lines and Instructions
Tangram pattern with black pieces and thin white-dotted lines. Tangrams, invented by the Chinese, are…

Tangram Pattern, Black with Small Dotted Lines and Instructions
Tangram pattern with black pieces and thin white-dotted lines. Tangrams, invented by the Chinese, are…

Tangram Pattern, Black with Solid Lines and Instructions
Tangram pattern with black pieces and thin white-dotted lines. Tangrams, invented by the Chinese, are…
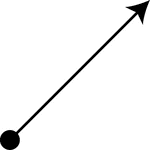
Ray Pointing Up and Right
A ray has one endpoint and extends indefinitely in the other direction. The ray in this illustration…
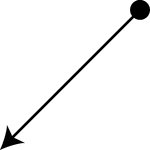
Ray Pointing Down and Left
A ray has one endpoint and extends indefinitely in the other direction. The ray in this illustration…