Semicircular Arch
"Semicircular arch, he center of which is in the same line with its springers." — The Encyclopedia…
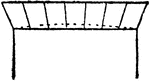
Flat Arch
"Flat arch, where the soffit is horizontal and sometimes slightly cambered (dotted line)." — The…
Water Level
"a, a, a, represents the water-level of a pond or reservoir upon elevated ground. From this pond a line…
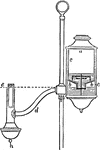
Reading Lamp
"An example of a form of reading lamp is seen here. The lamp is mounted on a standard on which it can…
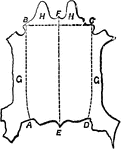
Hide Divisions
"The hides now come to be trimmed and prepared for tanning in the shape in which they are intended ultimately…
Ruling Pen
A form of pen used for drawing lines of even thickness. It commonly consists of two blades which hold…
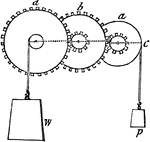
System of Wheels
"System of Wheels.—As the wheel and axle is only a modification of the simple lever, so a system…
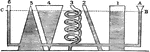
Water Pressure
"Suppose a number of vessels, of different shapes and sizes to have a communication between them, by…
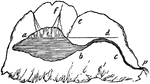
Intermitting Spring
"A mountain and spring, showing how the principle of the syphon operates to produce the effect described.…

Cup and Shilling
"The refraction of water is beautifully proved by the following simple experiment. Place an empty cup,…
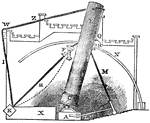
Telescope
"The following description of a section of Lord Rosse's telescope, though not so perfect as could be…
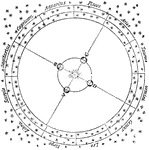
Zodiac Signs
"The twelve signs of the zodiac, together with the Sun, and the Earth revolving around him. When the…

Azimuth Compass
A compass placed in some convenient part of a ship on the midship line and provided with vanes, screws,…
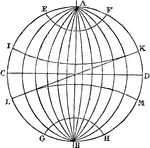
Earth Divisions
"The Earth, whose diameter is 7,912 miles, is represented by the globe, or sphere. The straight line…
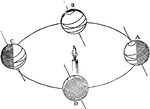
Earth Axis
"Now it is the inclination of the Earth's axis, as above described, which causes the lengths of the…

Earth Axis
"Now it is the inclination of the Earth's axis, as above described, which causes the lengths of the…
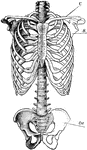
Skeletal Trunk
"The skeleton of the trunk and the limb arches seen from the front. C, clavicle; S, scapula; Oc, innominate…
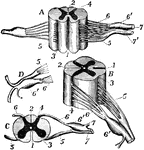
Nerve Roots
"The spinal cord and nerve-roots. A, a small portion of the cord seen from the ventral side; B, the…

Horizontal Line Diagram
In this figure BB is the base line; HH the common horizontal or vanishing line; C…
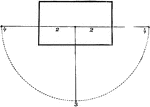
Parallel Perspective
This figure represents the whole of the points and lines requisite for working out a drawing in "parallel…
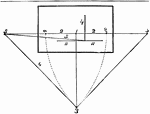
Angular Perspective
This figure comprises the whole of the points and lines preparatory to beginning a drawing in "angular…
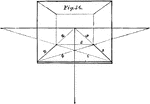
Parallel Perspective
The perspective shown in this plate is parallel perspective; and the subject here intended to be represented…
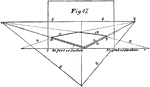
Angular Perspective
The perspective in this plate is "angular perspective," and the figure it represents is a flat square…
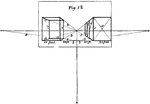
Parallel Perspective
Two upright oblong figures are here represented in parallel perspective. They may be imagined to resemble…

Angular Perspective
This object is a cube, having therefore all its faces of equal dimensions; and as both sides recede,…
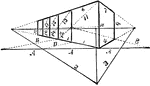
Angular Perspective
This cube has four additional cubes of equal dimensions. This is effected by first drawing the cube…
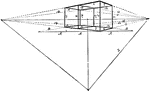
Angular Perspective
This figure differs from the others because they are solid cubes. Further, the geometrical scale is…
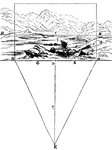
Distance
"A landscape is supposed to be viewed from the spot marked E; and that the spectator is desirous of…
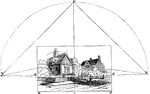
Vertical Line
That an accurate notion of the vertical line may be obtained, the plane of the picture must be supposed…
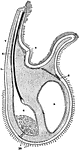
Brachiopoda
Diagrammatic section through an arm of the lophophore of Crania. 1, the lip; 2, the base of a tentacle…
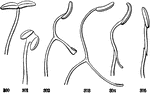
Stamens
Stamens of the mint family. Of a Monarda: the two anther-cells with bases divergent so that they are…
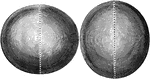
Oblate and Prolate Spheroid
The shape of the earth is that of a round ball or sphere slightly flattened at two opposite sides. Such…

Elizabeth, Countess of Devonshire
This is a line engraving by Sir Anthony Van Dyck. Pictures is Elizabeth, the wife of William Cavendish.…

Charles I Attended by the Marquis of Hamilton
This is a line engraving by Sir Anthony Van Dyck. The picture is one of many done for Charles I. The…
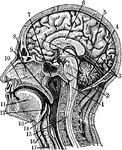
Sectional view of the Head
Section through the Head and Neck on the Median Line. 1. Medulla Oblongata 2. Pons 3. Right lobe of…

Cause of the Phases of the Moon
During new and full moon, the earth, moon, and sun are all in the same straight line, but, that during…
Five-ranked
Diagram of a shoot with its leaves 5-ranked, with a spiral line drawn from the attachment of one leaf…
Five-ranked
A ground-plan of the 5-ranked shoot; the section of the leaves; a dotted line drawn from the edge of…
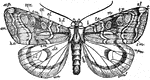
Owlet Moth
Wing of an owlet-moth, with all the markings defined and named.-Right wings: b, basal line; t.a., transverse…
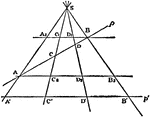
Cross-Ratio Four Points
The cross-ratio of four points in a line is equal to the cross-ratio of their projections on any other…
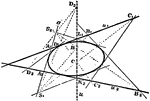
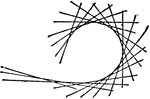
Second Order Curve
Five points are given, of which not three are in a line, a curve of second order may be drawn through…
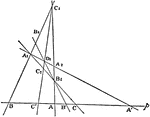
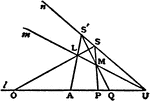
Involution
The three points in which any line cuts the sides of a triangle and the projections, from any point…
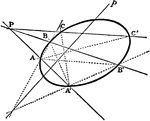
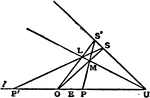
Conic Involution
The lines which join corresponding points in an involution on a conic all pass through a fixed point;…
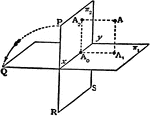
Perpendicular Planes
Two planes lie perpendicular to one another. A line perpendicular to plane 1 and a line perpendicular…

Line Projection
To find the projections of a line which joins two points, A, B given by their projections.
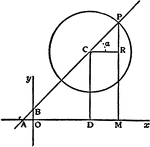
Straight Line
The straight line is the simplest type of locus and the simplest first degree equation.