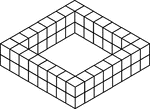
56 Stacked Congruent Cubes
Illustration of 56 congruent cubes stacked in twos in the shape of a square. A 3-dimensional representation…
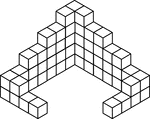
59 Stacked Congruent Cubes
Illustration of 59 congruent cubes stacked at various heights. A 3-dimensional representation on a 2-dimensional…
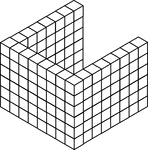
132 Stacked Congruent Cubes
Illustration of 132 congruent cubes stacked in 22 columns of 6 in the shape of a U. A 3-dimensional…
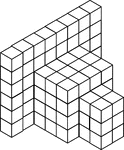
108 Stacked Congruent Cubes
Illustration of 108 congruent cubes stacked at various heights. A 3-dimensional representation on a…
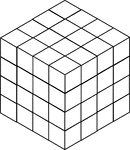
64 Stacked Congruent Cubes
Illustration of 64 congruent cubes stacked so they form a cube that measures 4 by 4 by 4. A 3-dimensional…
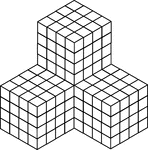
256 Stacked Congruent Cubes
Illustration of 256 congruent cubes stacked so they form 4 larger cubes that measures 4 by 4 by 4 each.…
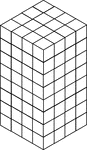
128 Stacked Congruent Cubes
Illustration of 128 congruent cubes stacked so they form a rectangular solid that measures 4 by 4 by…

39 Stacked Congruent Cubes
Illustration of 39 congruent cubes stacked at various heights. A 3-dimensional representation on a 2-dimensional…
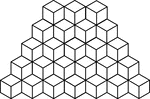
65 Stacked Congruent Cubes
Illustration of 65 congruent cubes stacked at heights increasing from 1 to 5 cubes. A 3-dimensional…
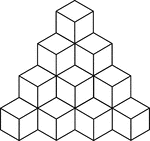
20 Stacked Congruent Cubes
Illustration of 20 congruent cubes stacked at heights increasing from 1 to 4 cubes. A 3-dimensional…

56 Stacked Congruent Cubes
Illustration of 56 congruent cubes stacked in heights of 1, 4, and 5 cubes that form a zigzag pattern.…
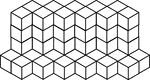
57 Stacked Congruent Cubes
Illustration of 57 congruent cubes stacked in heights of 1 and 5 cubes that form a zigzag pattern. A…
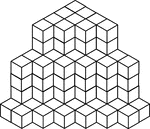
117 Stacked Congruent Cubes
Illustration of 117 congruent cubes stacked in columns of one, four, and six. A 3-dimensional representation…
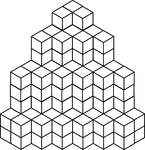
154 Stacked Congruent Cubes
Illustration of 154 congruent cubes stacked in columns increasing from one to four. A 3-dimensional…
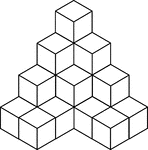
22 Stacked Congruent Cubes
Illustration of 22 congruent cubes stacked at various heights. A 3-dimensional representation on a 2-dimensional…
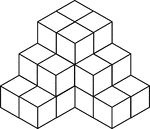
24 Stacked Congruent Cubes
Illustration of 24 congruent cubes stacked at various heights to resemble steps. A 3-dimensional representation…

27 Stacked Congruent Cubes
Illustration of 27 congruent cubes stacked to resemble a larger cube that measures three by three by…

36 Stacked Congruent Cubes
Illustration of 36 congruent cubes stacked to resemble a 1 by 1 by 1 cube on a 2 by 2 by 2 cube on a…
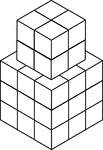
35 Stacked Congruent Cubes
Illustration of 35 congruent cubes stacked at various heights. A 3-dimensional representation on a 2-dimensional…
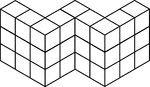
27 Stacked Congruent Cubes
Illustration of 27 congruent cubes stacked at various heights in the shape of a W. A 3-dimensional representation…

2 Narrow Cylinders on Their Sides
Illustration of 2 narrow right circular cylinders with equal heights (thickness) and different diameters.…
Concave Equilateral Decagon
A 5-point star made from a non-regular concave decagon in which all sides are equal in length.

Concave Equilateral Dodecagon
A 6-point star made from a non-regular concave dodecagon in which all sides are equal in length. There…
Circular Rosette With 4 Petals
Circular rosette with 6 petals in a circle. It is made by rotating circles about a fixed point. The…

Circular Design
Circular design made by rotating circles about a fixed point. The radii of the smaller circles is equal…

Circular Design
Circular design made by rotating circles about a fixed point. The radii of the smaller circles is equal…
Circular Rosette With 8 Petals
Circular rosette with 8 petals in a circle. It is made by rotating circles about a fixed point. The…

Circular Rosette With 16 Petals
Circular rosette with 16 petals in a circle. It is made by rotating circles about a fixed point. The…
Circular Rosette With 32 Petals
Circular rosette with 32 petals in a circle. It is made by rotating circles about a fixed point. The…

2 Intersecting Circles
2 congruent circles whose intersection includes a tangent circle with diameter equal to the radii of…
Reflected Arcs Of A Circle
A design created by dividing a circle into 4 equal arcs and reflecting each arc toward the center of…
Reflected Arcs Of 2 Circles In A Circle
A design created by dividing a circle into 4 equal arcs and creating a reflection of each arc toward…
Reflected Arcs Of 2 Circles
A design created by dividing a circle into 4 equal arcs and reflecting each arc toward the center of…
Reflected Arcs Of 2 Circles
A design created by dividing a circle into 4 equal arcs and reflecting each arc toward the center of…

Reflected Arcs Of 4 Circles In A Circle
A design created by dividing a circle into 4 equal arcs and creating a reflection of each arc toward…
Reflected Arcs Of 4 Circles In A Circle
A design created by dividing a circle into 4 equal arcs and creating a reflection of each arc toward…

Reflected Arcs Of 8 Circles In A Circle
A design created by dividing a circle into 4 equal arcs and creating a reflection of each arc toward…

Reflected Arcs Of 8 Circles
A design created by dividing a circle into 4 equal arcs and creating a reflection of each arc toward…
Circular Rosette With 3 Petals
Circular rosette with 3 petals. It is made by rotating circles about a fixed point. The radii of the…

Circular Rosette With 6 Petals
Circular rosette with 6 petals. It is made by rotating circles about a fixed point. The radii of the…

Circular Rosette With 12 Petals
Circular rosette with 12 petals. It is made by rotating circles about a fixed point. The radii of the…
Circular Rosette With 24 Petals
Circular rosette with 24 petals. It is made by rotating circles about a fixed point. The radii of the…
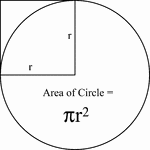
Area Of A Circle
An illustration used to show how the area of a circle is calculated. Area is equal to the product of…

6 Concentric Ellipses
An illustration of 6 concentric ellipses that are tangent at the end points of the vertical axes. The…

6 Concentric Ellipses
An illustration of 6 concentric ellipses that are tangent at the end points of the vertical axes, which…

5 Concentric Ellipses
An illustration of 5 concentric ellipses that are tangent at the end points of the vertical axes. The…
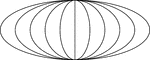
5 Concentric Ellipses
An illustration of 5 concentric ellipses that are tangent at the end points of the vertical axes, which…
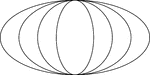
4 Concentric Ellipses
An illustration of 4 concentric ellipses that are tangent at the end points of the vertical axes. The…

4 Concentric Ellipses
An illustration of 4 concentric ellipses that are tangent at the end points of the vertical axes, which…
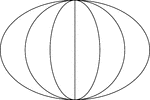
3 Concentric Ellipses
An illustration of 3 concentric ellipses that are tangent at the end points of the vertical axes, which…
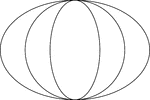
3 Concentric Ellipses
An illustration of 3 concentric ellipses that are tangent at the end points of the vertical axes. The…
2 Ellipses With Equal Vertical Axes
An illustration of 2 ellipses that have the equal vertical axes, but different horizontal axes. The…

2 Ellipses With Equal Vertical Axes
An illustration of 2 ellipses that have the equal vertical axes, but different horizontal axes. The…
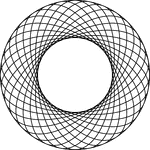
16 Rotated Concentric Ellipses
Illustration of 16 concentric congruent ellipses that are rotated about the center at equal intervals…
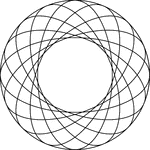
8 Rotated Concentric Ellipses
Illustration of 8 concentric congruent ellipses that are rotated about the center at equal intervals…
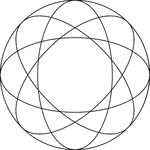
4 Rotated Concentric Ellipses
Illustration of 4 concentric congruent ellipses that are rotated about the center at equal intervals…
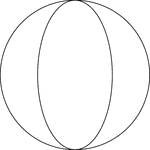
Ellipse Inscribed In A Circle
Illustration of an ellipse, whose major axis is vertical, inscribed in a circle whose diameter is equal…
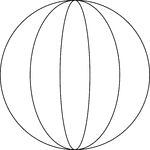
2 Ellipses Inscribed In A Circle
Illustration of 2 concentric ellipses, whose major axes are vertical, inscribed in a circle whose diameter…
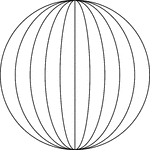
Ellipses Inscribed In A Circle
Illustration of concentric ellipses, whose major axes are vertical, inscribed in a circle whose diameter…
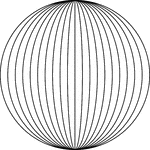
Ellipses Inscribed In A Circle
Illustration of concentric ellipses, whose major axes are vertical, inscribed in a circle whose diameter…