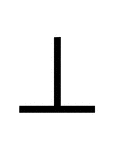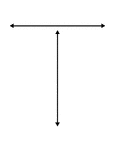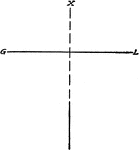
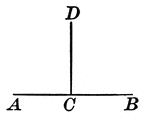
Intersecting Lines, 2 Perpendicular
2 intersecting lines, one of which is vertical and one of which is horizontal. The intersection forms…
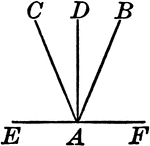
Bisected Angle
Illustration to show that if an angle is bisected, and if a line drawn through the vertex perpendicular…
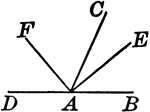
Bisected Angles
Illustration to show that the bisectors of two supplementary adjacent angles are perpendicular to each…
Bisected Angle
Illustration to show that the bisector of one of two vertical angles bisects the other.

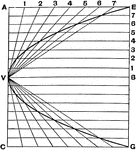
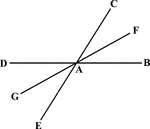
Bisected Angles
Illustration to show that the bisector of two pairs of vertical angles formed by two intersecting lines…
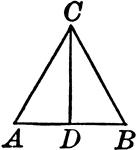
Bisected Vertical Angle of an Isosceles Triangle
Illustration to show that the bisector of the vertical angle of an isosceles triangle bisects the base,…
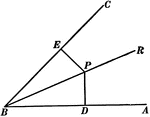
Perpendiculars To The Sides Of An Angle
Illustration used to show "The two perpendiculars to the sides of an angle from any point in its bisector…
Perpendiculars To The Sides Of An Angle
Illustration used to show "The two perpendiculars to the sides of an angle from any point not in its…
Right Angles With Same Vertex
An illustration showing when one straight line meets another straight line and makes the adjacent angles…
Angles Used to Illustrate Sum and Difference of Two Angles
Angles used to illustrate the sum and difference of two angles and trig identities.

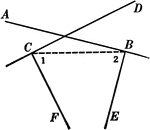
Supplementary and Right Angles
Illustration showing angles 1 and 2 are supplementary and angles ACD and DCB are supplementary. Also,…
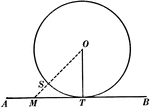
Tangent to Perpendicular Radius Circle Theorem
Illustration used to show that "A tangent to a circle is perpendicular to the radius drawn to the point…
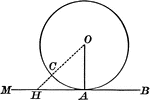
Circle With Tangent Line Drawn
Illustration of a circle with a tangent drawn - a straight line perpendicular to a radius at its extremity.
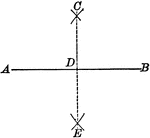
Construction of Bisecting a Given Line
Illustration of the construction used to bisect a given line.
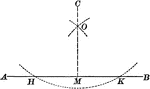
Construction of Perpendicular Upon a Given Line From an External Point
Illustration to let fall a perpendicular upon a given line from a given external point.
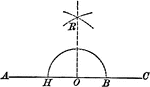
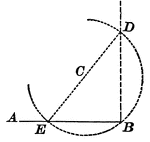
Construction of Perpendicular From a Given Point on a Straight Line
Illustration of the construction of a perpendicular to a line when given a point O on the straight line.
Construction of Perpendicular From a Given Point on a Straight Line
Illustration of the construction of a perpendicular to a line when given a point B on the straight line.
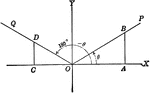
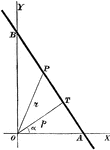
Coordinate Axis With Angles, Lines, and Perpendiculars Drawn
Coordinate axis with angle XOP equal to theta, Θ, and angle XOQ=180 - Θ. From any point in the terminal…

Coordinate Axis With Perpendiculars Drawn To Form Similar Right Triangles From Positive and Negative Theta, Θ
Angle XOP=Θ and angle XOQ=- Θ. From a point in the terminal side of each a perpendicular line is drawn…
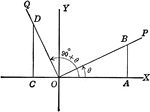
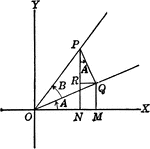
Coordinate Axis With Perpendiculars Drawn To Form Similar Right Triangles
Angle XOP=Θ and angle XOQ=90+Θ. From a point in the terminal side of each a perpendicular line is…
Intersecting Lines Corollary
Illustration used to prove the corollary that "Two lines perpendicular respectively to two intersecting…
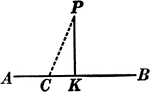
Perpendicular to Line Corollary
Illustration used to prove the corollary that "From a point outside a line there exists only one perpendicular…
Earth's Axis Perpendicular to Plane of Orbit
"The earth shown as it would be if its axis were perpendicular to the plane of the orbit." -Wiswell,…

Gules Shield
A heraldic shield with a red (gules) surface, which is represented by the perpendicular lines, drawn…
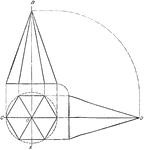
Projection Of Hexagonal Pyramid
Illustration of the projection of a hexagonal pyramid that is in a right position.
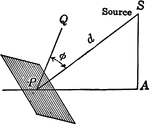
Illumination of a Surface When the Surface is not Perpendicular to the Source
Illustration modeling the illumination on a surface when the surface is not perpendicular to hte rays…
Extension Ladder
Illustration of an extension ladder. If ladder is leaned against a building, it will form a right triangle…
Leaning Ladder
Illustration of a ladder that is not perpendicular to the ground. If it is set on the ground and leaned…
Leaning Ladder
Illustration of a ladder that is not perpendicular to the ground. If it is set on the ground and leaned…
Leaning Ladder
Illustration of a ladder that is not perpendicular to the ground. If it is set on the ground and leaned…

Leaning Ladder
Illustration of a ladder that is not perpendicular to the ground. If it is set on the ground and leaned…

Ladder Leaning Against a Building
Illustration of a ladder leaning against the side of a building (wall) to form a right triangle .

Ladder Leaning Against a Tree
Illustration of a ladder leaning against a palm tree, that is perpendicular to the ground, to form a…

Ladder Leaning Against a Tree
Illustration of a ladder leaning against a palm tree, that is perpendicular to the ground, to form a…
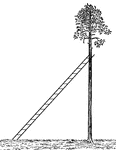
Ladder Leaning Against a Tree
Illustration of a ladder leaning against a palm tree, that is perpendicular to the ground, to form a…
Ladder Leaning Against a Tree
Illustration of a ladder leaning against a palm tree, that is perpendicular to the ground, to form a…
2 Ladders Leaning Against a Tree
Illustration of 2 ladders leaning against opposite sides of a palm tree to form similar right triangles.…

3 Ladders Leaning Against a Wall
Illustration of 3 ladders leaning against the side of a building (wall) to form right triangles. The…
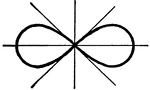
Lemniscate
A Lemniscate is, in general, a curve generated by a point moving so that the product of its distances…
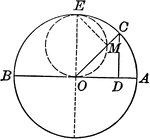
Circle Made by Ends of a Line Touching Two Fixed Lines Perpendicular to Each Other
Illustration showing a line that moves so that its ends constantly touch two fixed lines which are perpendicular…
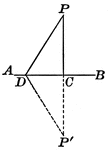
Perpendicular Line Drawn To a Given Line From an External Point
Illustration showing that the perpendicular is the shortest line that can be drawn to a straight line…
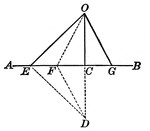
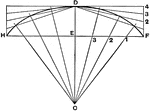
Lines Drawn From the Same Point in a Perpendicular to a Given line, Cutting Off Segments
Illustration showing two straight lines drawn from the same point in a perpendicular to a given line,…
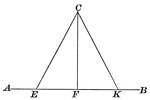
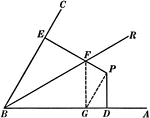
Lines Drawn to Another Line to Form Triangle
Illustration of two straight lines drawn from a point in a perpendicular to a given line, cutting off…
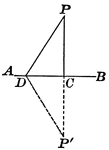
Perpendicular Line Drawn to a Given Line from an External Point
Illustration showing only one perpendicular can be drawn to a given line from a given external point.
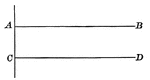
Parallel Lines
Illustration showing two straight lines in the same plane perpendicular to the same straight line are…
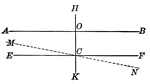
Parallel Lines
Illustration showing if a straight line is perpendicular to one of two parallel lines, it is perpendicular…
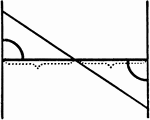
Parallel Lines Cut By a Perpendicular And Transversal
Illustration showing two parallel vertical lines cut by a perpendicular line and a transversal. Congruent…
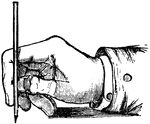
Penmanship
The correct position when the pen is at the bottom of an extended letter below the line, the pen being,…
Perpendicular Line Drawn From Point P to Line RS
A perpendicular line drawn from point P to straight line RS.