Construction Of An Octagon
An illustration showing how to construct an octagon on a given line. "Prolong AB to C. With B as center…
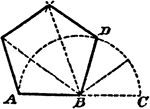
Construction Of An Octagon From a Square
An illustration showing how to construct a regular octagon from a square by cutting off the corners…
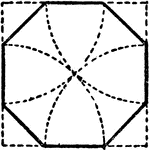
Area Of Regular Polygon Proof
An illustration showing that the area of a regular polygon is equal to the area of a triangle whose…
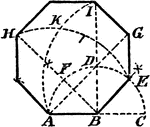
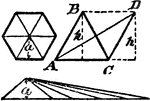
Construction Of A Regular Polygon On A Line
An illustration showing how to construct a regular polygon on a given line without resort to its center.…
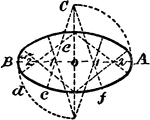
Construction Of An Isometric Ellipse
An illustration showing how to construct an isometric ellipse by compass and six circle arcs. "Divide…
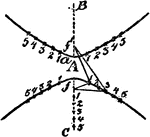
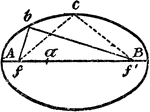
Construction Of A Hyperbola
An illustration showing how to construct a hyperbola by plotting. "Having given the transverse axis…
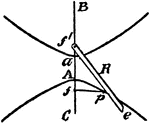
Construction Of A Hyperbola
An illustration showing how to construct a hyperbola by a pencil and a string. "Having given the transverse…
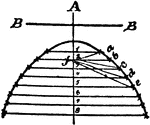
Construction Of A Parabola
An illustration showing how to construct a parabola by plotting. "Having given the axis, vertex, and…
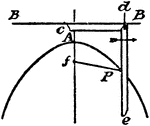
Construction Of A Parabola
An illustration showing how to construct a parabola using a pencil and a string. "Having given the two…

Construction Of Shield's Anti-friction Curve
An illustration showing how to construct Shield's anti-friction curve. "R represents the radius of the…
Construction Using Isometric Perspective
An illustration showing how to use isometric perspective. "This kind of perspective admits of scale…
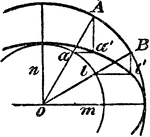
Construction Of An Ellipse
An illustration showing how to construct an ellipse. "With a as a center, draw two concentric circles…
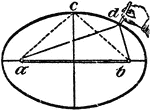
Construction Of An Ellipse
An illustration showing how to construct an ellipse using a string. "Having given the two axes, set…
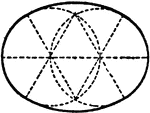
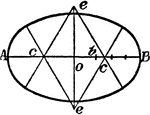
Construction Of An Ellipse
An illustration showing how to construct an ellipse using circle arcs. "Divide the long axis into three…
Construction Of An Ellipse
An illustration showing how to construct an ellipse using circle arcs. "Given the two axes, set off…
Construction Of An Ellipse
An illustration showing how to construct an ellipse. Given the two axes, set off half the long axis…
Construction Of An Ellipse Tangent To Two Parallel Lines
An illustration showing how to construct an ellipse parallel to two parallel lines A and B. "Draw a…
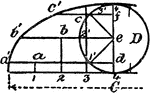
Construction Of A Cycloid
An illustration showing how to construct a cycloid. "The circumference C=3.14D. Divide the rolling circle…

Construction Of An Evolute Of A Circle
An illustration showing how to construct an evolute of a circle. "Given the pitch p, the angle v, and…
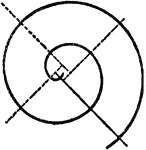
Construction Of A Spiral
An illustration showing how to construct a spiral with compasses and four centers. "Given the pitch…

Construction Of A Parabola
An illustration showing how to construct a parabola. "Given the vertex A, axis x, and a point P. Draw…
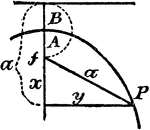
Construction Of A Parabola
An illustration showing how to construct a parabola. "Given the axis of ordinate B, and vertex A. Take…
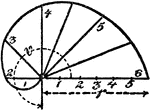
Construction Of An Arithmetic Spiral
An illustration showing how to construct an arithmetic spiral. "Given the pitch p and angle v, divide…

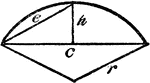
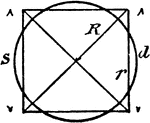
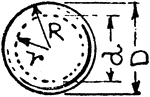
Radius, Diameter, and Chord In A Circle
An illustration showing a circle with radius r, diameter d, and chord c.
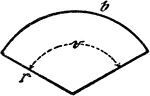
Circle Sector
An illustration showing a circle sector with radius r, center/central angle v, and length of circle…

Circle Sector
An illustration showing a circle sector with center/central angle v and polygon angle w.
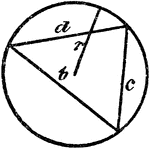
Triangle Inscribed In A Circle
An illustration showing a triangle with sides b, c, and d inscribed in a circle with radius r.
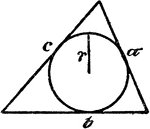
Circle Inscribed In A Triangle
An illustration showing a circle with radius r inscribed in a triangle with sides a, b, and c.
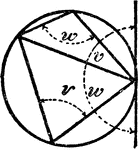
Quadrilateral Inscribed In A Circle
An illustration showing a quadrilateral inscribed in a circle that is tangent to a line.
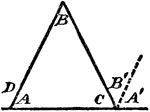
Exterior And Interior Angles Of A Triangle
An illustration showing a triangle with interior angles A, B, C, and exterior angles D, and A' + B'.
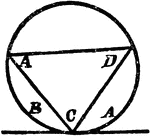
Triangle Inscribed In A Circle
An illustration showing a triangle with angles A, C, and D inscribed in a circle which is tangent to…
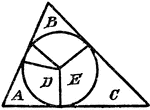
Circle Inscribed In A Triangle
An illustration showing a circle with sectors D and E inscribed in a triangle with angles, A, B, and…

Geometry
Two students drawing geometrical shapes on the chalkboard. A student is also using a scale while students…

Area of Hexagon
Illustration showing how to find the area of a hexagon using the triangles that make it up.
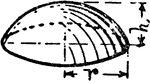
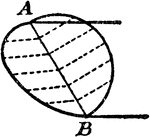
Area of Sphere
"It is found that the cord covering the curved surface is twice as long as the one covering the flat…

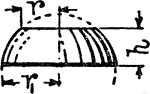
Area of Sphere
"The bases of the pyramids are considered as forming the surface of the sphere, while the altitude of…
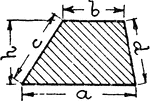
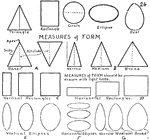
Forms
Showing different types of forms or shapes: rectangle, right triangle, acute triangle, and obtuse triangle.
Parallel Prisms
Showing different types of parallel prisms: rectangular, right triangular, acute triangular, and obtuse…
Oblique Prisms
Showing different types of oblique prisms: rectangular, right triangular, acute triangular, and obtuse…
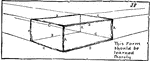
Rectangular Prism
A rectangular prism with labeled sides: AAAA are the four vertical parallel corners. BBBB and CCCC are…
Parallel Prisms
Types of parallel prisms: right triangular prism, isosceles triangular prism, rectangular prism, cylinder.
Oblique Prisms
Types of oblique prisms: right triangular prism, isosceles triangular prism, rectangular prism, cylinder.
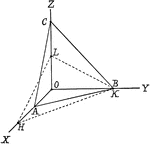
Plane
Illustration showing a how in "analytic geometry it is customary to specify the position of a plane…