A board game for two players.

"Backgammon, a game played by two persons upon a table or board made for the purpose, with pieces or…

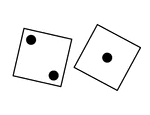
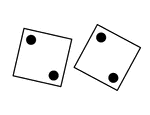
Small cubes, used in gaming, by being thrown from a box.
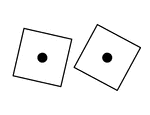
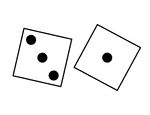
Pair of thrown dice showing two ones.

A small cubed marked on its faces with spots numbering from one to six, used in gaming from being thrown…

An orthographic illustration of a die displaying sides 1, 2, and 4.

An orthographic illustration of a die displaying sides 1, 3, and 2.

An orthographic illustration of a die displaying sides 1, 4, and 5.

An orthographic illustration of a die displaying sides 1, 5, and 3.
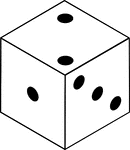
An orthographic illustration of a die displaying sides 2, 1, and 3.

An orthographic illustration of a die displaying sides 2, 3, and 6.

An orthographic illustration of a die displaying sides 2, 4, and 1.

An orthographic illustration of a die displaying sides 2, 6, and 4.

An orthographic illustration of a die displaying sides 3, 1, and 5.
An orthographic illustration of a die displaying sides 3, 2, and 1.

An orthographic illustration of a die displaying sides 3, 5, and 6.

An orthographic illustration of a die displaying sides 3, 6, and 2.

An orthographic illustration of a die displaying sides 4, 1, and 2.

An orthographic illustration of a die displaying sides 4, 2, and 6.

An orthographic illustration of a die displaying sides 4, 5, and 1.

An orthographic illustration of a die displaying sides 4, 6, and 5.

An orthographic illustration of a die displaying sides 5, 1, and 4.

An orthographic illustration of a die displaying sides 5, 3, and 1.

An orthographic illustration of a die displaying sides 5, 4, and 6.

An orthographic illustration of a die displaying sides 5, 6, and 3.

An orthographic illustration of a die displaying sides 6, 2, and 3.

An orthographic illustration of a die displaying sides 6, 3, and 5.

An orthographic illustration of a die displaying sides 6, 4, and 2.