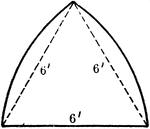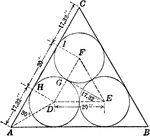
Circles Enclosed in Equilateral Triangle
Illustration of three circles enclosed in an equilateral triangle.
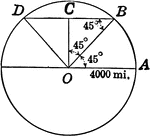
Circles With Radius 4000 and Enclosed Triangle
Illustration of circle with radius of 4000, and triangle with 45 degree angle enclosed.

Triangle Inscribed in Circle
Illustration of triangle inscribed in circle. Or, circle circumscribed about triangle.
Triangle Construction When Given 2 Angles and Included Side
Triangle construction when given two angles and the included side.
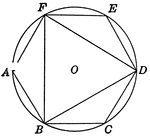
Hexagon Inscribed in Circle by Construction
Illustration of regular hexagon and triangle inscribed in circle.

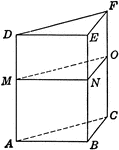
Prismatoid With Triangular Faces
An illustration of a prismatoid with triangular faces and points labeled.
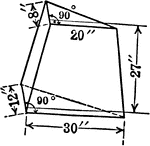
Pyramid Frustum With Triangular Bases and Height of 27 inches
An illustration of a pyramid with the top cut off by a plane parallel to the base. The remaining part…
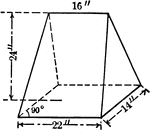
Pyramid Frustum With Triangular Bases and Height of 27 inches
An illustration of a pyramid with the top cut off by a plane parallel to the base. The remaining part…
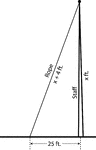
Right Triangle Formed by Flagpole (x feet high) and Ground With Rope (x+4 feet)
An illustration of a right triangle made up of a flagpole, rope, and the ground. Illustration could…
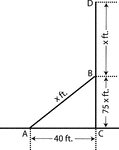
Right Triangle With Sides x, 75, and 40
An illustration of a right triangle with sides, 40, 75, and x. Additional height of x is added to 75.…
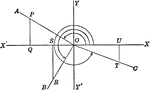
Reference Angles/Triangles Formed by Angles in Quadrants
Lines drawn to horizontal to form triangle ratios (reference triangles, angles).
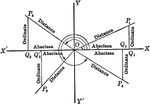
Reference Angles/Triangles Formed by Angles in Quadrants With Labels
Lines drawn to horizontal to form triangle ratios (reference triangles, angles). Axes, quadrants, abscissa,…
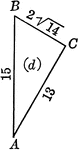
Right Triangle with leg 13 and hypotenuse 15
Right triangle ABC with angles A, B, C labeled and leg of 13 with hypotenuse of 15.
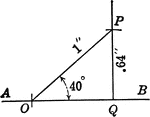
Right Triangle With Sides .64 and 1 and Angle of 40 degrees
Right triangle OQP with angle of 40 degrees, height of .64 inches, and hypotenuse of 1 inch.
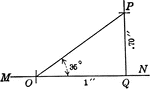
Right Triangle With Sides .7 and 1 and Angle of 35 degrees
Right triangle OQP with angle of 35 degrees, height of .70 inches, and leg of 1 inch.

Special Right Triangle with Angles 45, 45, 90 degrees
Special right triangle with angles 45 degrees, 45 degrees, and 90 degrees with side measures/relationships…
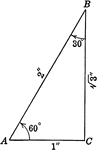
Special Right Triangle with Angles 30, 60, 90 degrees
Special right triangle with angles 30 degrees, 60 degrees, and 90 degrees with side measures/relationships…
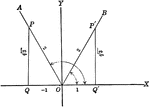
Trigonometric Reference Triangles/Angles (60 degrees) Drawn in Quadrants
Trigonometric reference triangles/angles drawn for 60 degree reference angel in quadrants I and II.

Trigonometric Reference Triangles/Angles Drawn in Quadrants
Trigonometric reference triangles/angles drawn for reference angel in quadrants I and II. This illustration…
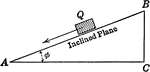
Inclined Plane Forming Right Triangle
Inclined plane forming right triangle showing the velocity of a body sliding a distance,s, down a smooth…
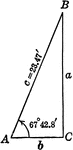
Right Triangle ABC With Angle 67 degrees 42.8 minutes and Hypotenuse 23.47 ft.
Right triangle ABC with a base angle of 67 degrees 4208 minutes and a hypotenuse of 23.47 ft.

Right Triangle ABC With Leg 23.85 ft. and Hypotenuse 35.62 ft.
Right triangle ABC with a leg of 23.85 feet and a hypotenuse of 35.62 feet.
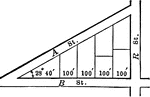
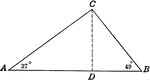
Triangular City Block With Angles and Lengths
Illustration showing an angle of 23 degrees 40 minutes making a triangle in a city block and marking…
Survey of Lake Front in Chicago
Illustration showing a survey on the lake front in Chicago with distances and angle measures shown.
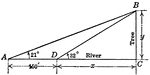
Right Triangle For Finding Distance Across a River
Right triangle ABC with angles A, B, C to be used for finding distance across a river. This is a trigonometry…
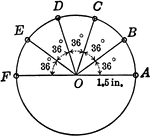
Circle With 36 degree Angles and Radius 1.5 in.
Circle with 36 degree angles marked. This diagram can be used with the following trig problem: Locate…
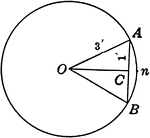
Circle With a Chord of 2 ft. and a Radius of 3 ft.
Circle with chord AB=2 ft. and radius OA = 3 ft.. Triangle AOC is a right triangle. Angle AOC=half angle…
Roof With 30 degree Inclination for Trigonometry Triangle Problems
Roof with a slope of 30 degrees. Angle theta is the inclination to the horizontal of the line AB, drawn…
Two Squares With Sides of Lengths 3,4,5 Placed at Right Angles to Each Other
Two set squares, whose sides are 3,4, and 5 in., are placed so that their 4-in. sides and right angles…
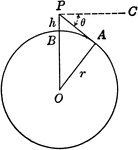
Circle With Center o and Radius r with point P
Circle modeling the earth. O is the center of the earth, r the radius of the earth, and h the height…
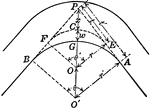
Curve in Pavement of Road
Illustration of blueprint used by highway engineers to widen the pavement on the inside of the curve…
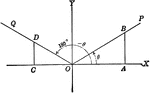
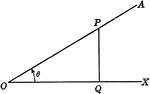
Coordinate Axis With Angles, Lines, and Perpendiculars Drawn
Coordinate axis with angle XOP equal to theta, Θ, and angle XOQ=180 - Θ. From any point in the terminal…
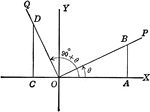
Coordinate Axis With Perpendiculars Drawn To Form Similar Right Triangles
Angle XOP=Θ and angle XOQ=90+Θ. From a point in the terminal side of each a perpendicular line is…

Coordinate Axis With Perpendiculars Drawn To Form Similar Right Triangles From Positive and Negative Theta, Θ
Angle XOP=Θ and angle XOQ=- Θ. From a point in the terminal side of each a perpendicular line is drawn…
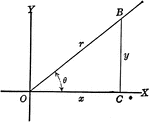
Right Triangle OCB With, x, y, and r shown
Right triangle OCB that can be used to show the relationships between x, y, r, and Θ.
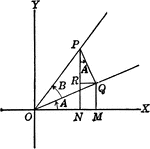
Angles Used to Illustrate Sum and Difference of Two Angles
Angles used to illustrate the sum and difference of two angles and trig identities.
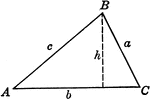
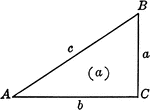
Triangle ABC With Height h
Triangle ABC with sides a,b,c labeled and angles A,B,C labeled and h labeled as height.
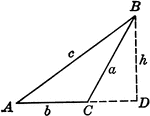
Obtuse Triangle ABC With Height h
Triangle ABC with sides a,b,c labeled and angles A,B,C labeled and h labeled as height.
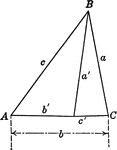
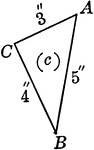
Triangles ABC and ABC'
Triangle ABC and triangle ABC'. This illustration could be used to demonstrate the law of sines.
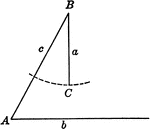
Ambiguous Case of Law of Sines Triangle
Illustration showing ambiguous case when the solution is not a triangle using law of sines.
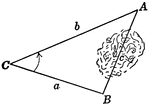
Oblique Triangle for Distance Across Lake
Illustration of oblique triangle used to find distance across a lake.
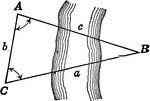
Oblique Triangle for Distance Across a River
Illustration of oblique triangle used to find distance across a river.
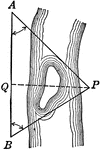
Oblique Triangle for Distance Across a River
Illustration of oblique triangle used to find distance across a river.
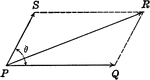
Resultant Vectors
Illustration of the resultant vector when two vectors are acting upon a body at point P.
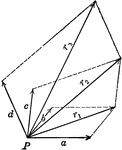
Resultant Vector From 4 Forces
Illustration of the resultant vector when four vectors are acting upon a body at point P.
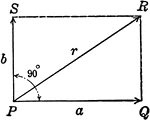
Resultant Vector With Vectors at 90 degrees
Illustration of the resultant vector when two vectors are acting upon a body at point P at 90 degrees.
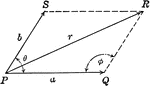
Resultant Vector With Vectors at Angle Ǝ
Illustration of the resultant vector when two vectors are acting upon a body at point P at Ǝ degrees.