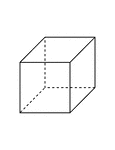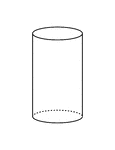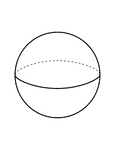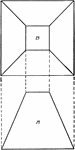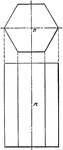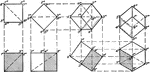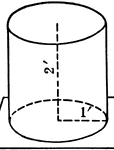
Right Circular Cylinder With 1 ft. Radius and 2 ft. height.
Right circular cylinder with a radius of 1 foot and a height/altitude of 2 feet.
Side And Top Views Of A Cylinder
Illustration of the plan and shaded elevation of a cylinder. The cylinder is viewed from the side and…
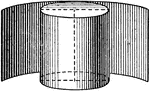
Surfaces Of A Cylinder
Illustration of a cylinder showing, "If a piece of paper is fitted to cover the convex surface of a…
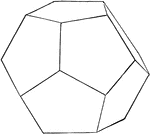
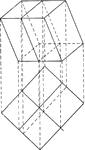
Regular Dodecahedron
Illustration of a regular dodecahedron. A regular dodecahedron is a polyhedron with twelve equal pentagonal…
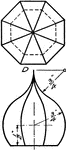
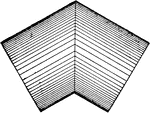
Development Exercise of Dome and True Shape of Hip
A development or rolled out image exercise problem of the dome and finding the true shape of the hip,…
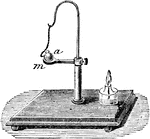
Expansion of Solids
"The expansion of solids by heat is clearly shown by the following experiment: m represents a ring of…
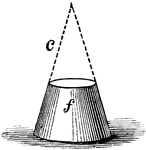
Frustum of a Cone
"The part of any solid between two planes, which may be either parallel or inclined to each other: as,…
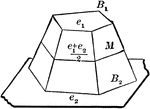
Volume of Frustum of a Pyramid
Diagram used to prove the theorem: "The volume of the frustum of a pyramid (cone) is equal to the sum…
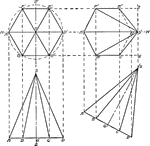
Development of Hexagonal Pyramid
An image of a hexagonal pyramid stretched out. The length of the edges are equal plane, and intersects…
Frustum of Hexagonal Pyramid
Illustration of a frustum of a hexagonal pyramid (including cross-section).

Intersection of Hexagonal Pyramid and a Plane
Illustration of the intersection of a hexagonal pyramid and a plane.
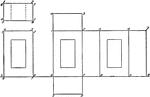
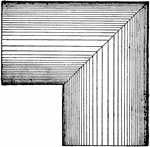
Development of Hollow Rectangular Prism
Pattern that can be used to make a hollow rectangular prism. Development of hollow rectangular prism.
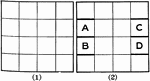
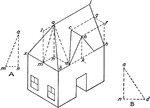
Pattern To Make A House
Illustration of pattern showing steps to make a house. The house is a composite figure made up of a…
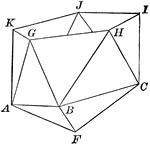
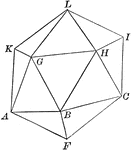
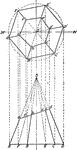
Part of an Icosahedron
Illustration of the bottom part of an icosahedron. The base consists of a regular pyramid, upon which…
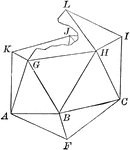
Partial Construction of an Icosahedron
Illustration of the steps to a construction of an icosahedron. The base consists of a regular pyramid,…
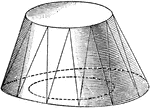
Practical Projection Of An Irregular Solid
Illustration showing a general way the method of arranging the triangles on the irregular surface of…
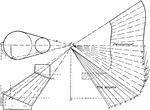
Oblique Cone by Triangulation Connecting to Two Parallel Pipes of Different Diameters
"An oblique cone connecting two parallel pipes of different diameters... the true size of the base is…
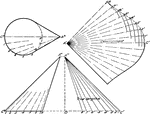
Development of Oblique Cone by Triangulation
A development or rolled out oblique cone using triangulation. The method of triangulation is done by…
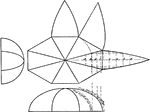
Development of Octagonal Dome
A stretched out image of the octagonal dome by using projection or with dividers to create a five-piece…
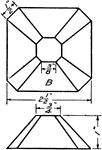
Development Exercise of Octagonal Light Shade
A problem exercise creating a stretched out or developed image of the octagonal light shade by using…
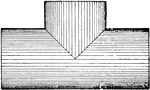
Plane Intersecting Octagonal Prism
Illustration showing the intersection of a plane with an octagonal prism.
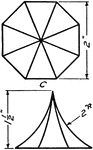
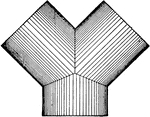
Development Exercise of Octagonal Roof and True Shape of Rafter
Problem exercise in drawing a development or a stretchout image of the octagonal roof and finding the…
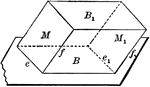
Equal and Parallel Opposite Faces of a Parallelopiped
Diagram used to prove the theorem: "The opposite faces of a parallelopiped are equal and parallel."
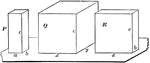
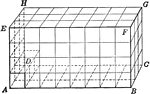
Relationship Between 2 Parallelopipeds With Equal Altitudes
Diagram used to prove the theorem: "The rectangular parallelopipeds which have two dimensions in common…

Relationship Between Dimensions of Parallelopipeds
Diagram used to prove the theorem: "The rectangular parallelopipeds are to each other as the product…
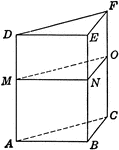
Volume of Parallelopiped
Diagram used to prove the theorem: "The volume of a any parallelopiped is equal to the product of its…
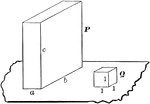
Volume of Rectangular Parallelopiped
Diagram used to prove the theorem: "The volume of a rectangular parallelopiped is equal to the product…

Frustum of Pentagonal Pyramid
Illustration of a frustum of a pentagonal pyramid (including cross-section).
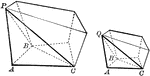
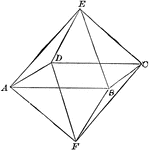
Two Similar Polyhedrons
Diagram used to prove the theorem: "Two similar polyhedrons may be decomposed into the same number of…

Intersecting Prism and Cylinder
Illustration of the intersection of an octagonal prism and a cylinder. The figures intersect at an oblique…
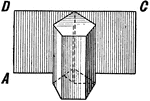
Surfaces Of A Prism
Illustration of a pentagonal prism showing, "If a piece of paper is fitted to cover the convex surface…